વૈકલ્પિક પ્રવાહો માટે તબક્કો શિફ્ટ

વૈકલ્પિક પ્રવાહો સમાન આવર્તન તેઓ માત્ર કંપનવિસ્તારમાં જ નહીં, પણ તબક્કામાં પણ એકબીજાથી અલગ હોઈ શકે છે, એટલે કે, તેઓ તબક્કા-સ્થળાંતર થઈ શકે છે.

જો બે વૈકલ્પિક પ્રવાહો એક સાથે ટોચના મૂલ્યો સુધી પહોંચે છે અને એક સાથે શૂન્ય મૂલ્યોમાંથી પસાર થાય છે, તો આ પ્રવાહો તબક્કામાં છે. આ કિસ્સામાં, પ્રવાહો વચ્ચેનો તબક્કો શૂન્ય છે (ફિગ. 1, એ).

જો કે, એવા કિસ્સાઓ છે જ્યારે આ પ્રવાહોના કંપનવિસ્તાર (અને શૂન્ય) ના મૂલ્યો સમયસર એકબીજા સાથે મેળ ખાતા નથી, એટલે કે, ત્યાં એક અથવા બીજા તબક્કાની પાળી છે જે શૂન્યની બરાબર નથી. અંજીરમાં. 1b એવા પ્રવાહો દર્શાવે છે જે સમયગાળાના એક ક્વાર્ટર (T/4) દ્વારા તબક્કો શિફ્ટ થાય છે.

તબક્કાની પાળી સામાન્ય રીતે ગ્રીક અક્ષર φ દ્વારા સૂચવવામાં આવે છે અને ઘણી વખત ડિગ્રીમાં દર્શાવવામાં આવે છે, એમ ધારીને કે સમગ્ર સમયગાળો 360° છે, જેમ કે એક સંપૂર્ણ ક્રાંતિ 360°ને અનુરૂપ છે. આમ, સમયગાળાના એક ક્વાર્ટર દ્વારા તબક્કાની શિફ્ટ φ = 90 ° દ્વારા સૂચવવામાં આવે છે, અને જ્યારે તબક્કાઓ અડધા સમયગાળા દ્વારા સ્થાનાંતરિત થાય છે, ત્યારે તેઓ φ = 180e લખે છે.

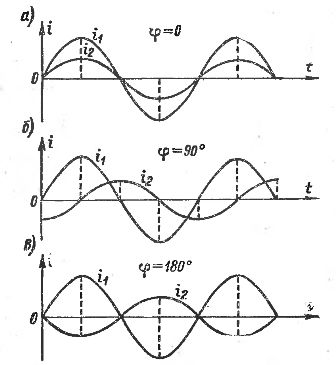
ચોખા. 1. બે વૈકલ્પિક પ્રવાહો વચ્ચે વિવિધ તબક્કામાં ફેરફાર

વૈકલ્પિક વર્તમાન T અને કોણ 360 ° વચ્ચેનો સંબંધ પ્રયોગ પરથી સ્થાપિત કરી શકાય છે જેમાં એક સમાન ચુંબકીય ક્ષેત્રમાં કોઇલ (અથવા કોઇલ) ના સમાન પરિભ્રમણ સાથે વૈકલ્પિક સાઇનુસાઇડલ EMF મેળવવામાં આવે છે. આ કિસ્સામાં, કોઇલના એક વળાંક માટે, એટલે કે. 360 °ના ખૂણા દ્વારા તેના પરિભ્રમણ દરમિયાન, EMF એક સંપૂર્ણ સાઇનસોડલ ઓસિલેશન બનાવે છે. આમ, વાસ્તવમાં, સમયગાળો T 360 ° ના ખૂણાને અનુરૂપ છે.

તે જ વૈકલ્પિક પ્રવાહ માટે ગાણિતિક અભિવ્યક્તિમાંથી, એટલે કે તેના સમીકરણમાંથી અનુસરે છે. જો વૈકલ્પિક પ્રવાહ શૂન્ય તબક્કામાંથી તેનું પરિવર્તન શરૂ કર્યું જ્યારે t = 0, ωt = 0 અને sin ωt = 0, એક સમયગાળા પછી તે બહાર આવશે

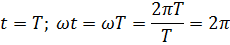
આ બિંદુએ તબક્કો કોણ 2π રેડિયન અથવા 360 ° છે અને તેથી sin ωt = sin 2π = sin 360 ° = 0. જ્યારે કોણ 0 થી 2π રેડિયન અથવા 360 ° સુધી બદલાય છે, ત્યારે સાઈન તેના ફેરફારોનું સંપૂર્ણ ચક્ર બનાવે છે. તદનુસાર, વૈકલ્પિક પ્રવાહ એક સંપૂર્ણ ઓસિલેશન બનાવે છે.

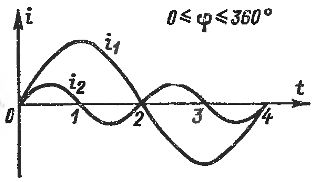
તે યાદ રાખવું આવશ્યક છે કે માત્ર સમાન આવર્તનના પ્રવાહોમાં સારી રીતે વ્યાખ્યાયિત તબક્કાની પાળી હોઈ શકે છે. પ્રવાહોની વિવિધ ફ્રીક્વન્સીઝ પર, તેમની વચ્ચેનો તબક્કો સ્થિર નથી, પરંતુ દરેક સમયે બદલાય છે. ઉદાહરણ તરીકે, ફિગમાં બતાવેલ કરંટ i1 અને i2 માટે. 2 અને બેના પરિબળ દ્વારા એકબીજાથી ભિન્ન ફ્રિક્વન્સી સાથે, પોઈન્ટ 0, 1, 2, 3, 4 દ્વારા દર્શાવવામાં આવેલ સમયની તબક્કો પર તબક્કો શિફ્ટ અનુક્રમે 0 છે; 90; 180; 270; 360 °, એટલે કે વર્તમાન i1 ના એક સમયગાળા દરમિયાન, φ નું મૂલ્ય 0 થી 360 ° સુધી બદલાય છે.

ચોખા. 2. વિવિધ ફ્રીક્વન્સીઝના પ્રવાહો વચ્ચે વેરિયેબલ ફેઝ શિફ્ટ

પ્રવાહો વચ્ચેના તબક્કાના શિફ્ટ વિશે જે કહેવામાં આવે છે તે બધું વોલ્ટેજ અને ઇલેક્ટ્રોમોટિવ દળોને પણ લાગુ પડે છે. નીચે આપણે એવા કિસ્સાઓ ધ્યાનમાં લઈશું કે જ્યાં વોલ્ટેજ અને વર્તમાન વચ્ચે તબક્કો શિફ્ટ હશે.