ડીસી મોટરનું સ્પીડ કંટ્રોલ
 ઇલેક્ટ્રોમિકેનિકલ લાક્ષણિકતા સમીકરણમાંથી કાયમી એન્જિન સ્વતંત્ર ઉત્તેજના, તે અનુસરે છે કે તેના કોણીય વેગને નિયંત્રિત કરવાની ત્રણ સંભવિત રીતો છે:
ઇલેક્ટ્રોમિકેનિકલ લાક્ષણિકતા સમીકરણમાંથી કાયમી એન્જિન સ્વતંત્ર ઉત્તેજના, તે અનુસરે છે કે તેના કોણીય વેગને નિયંત્રિત કરવાની ત્રણ સંભવિત રીતો છે:
1) આર્મેચર સર્કિટમાં રિઓસ્ટેટના પ્રતિકાર મૂલ્યને બદલીને નિયમન,
2) મોટર F ના ઉત્તેજના પ્રવાહને બદલીને નિયમન,
3) મોટર U... આર્મેચર સર્કિટ વર્તમાન AzI અને મોટર દ્વારા વિકસાવવામાં આવેલ ક્ષણ M તેના શાફ્ટ પરના ભારની તીવ્રતા પર જ આધાર રાખે છે.
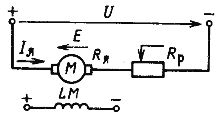
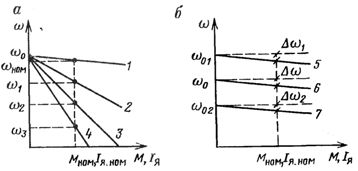
આર્મેચર સર્કિટમાં પ્રતિકાર બદલીને ડીસી મોટરની ઝડપને નિયંત્રિત કરવાની પ્રથમ પદ્ધતિનો વિચાર કરો... આ કેસ માટે મોટર સર્કિટ રેખાકૃતિ ફિગમાં બતાવવામાં આવી છે. 1, અને ઇલેક્ટ્રોમિકેનિકલ અને મિકેનિકલ લાક્ષણિકતાઓ ફિગમાં બતાવવામાં આવી છે. 2, એ.
ચોખા. 1. સ્વતંત્ર ઉત્તેજના સાથે ડીસી મોટરનું સર્કિટ ડાયાગ્રામ
ચોખા. 2. વિવિધ આર્મેચર સર્કિટ પ્રતિકાર (a) અને વોલ્ટેજ (b) પર ડીસી મોટરની યાંત્રિક લાક્ષણિકતાઓ
આર્મેચર સર્કિટમાં રિઓસ્ટેટના પ્રતિકારને બદલીને, કૃત્રિમ લાક્ષણિકતાઓ — ω1, ω2, ω3 દ્વારા ઇલેક્ટ્રિક મોટરની વિવિધ કોણીય ગતિ મેળવવા માટે નજીવા લોડ પર શક્ય છે.
ચાલો મુખ્ય તકનીકી અને આર્થિક સૂચકાંકોનો ઉપયોગ કરીને ડીસી મોટર્સના કોણીય વેગને નિયંત્રિત કરવાની આ પદ્ધતિનું વિશ્લેષણ કરીએ. ગોઠવણની આ પદ્ધતિ વ્યાપક શ્રેણીમાં લાક્ષણિકતાઓની જડતાને બદલે છે, પછી નજીવા કરતાં અડધાથી ઓછી ઝડપે, એન્જિનની કામગીરીની સ્થિરતા તીવ્રપણે બગડે છે. આ કારણોસર, ઝડપ નિયંત્રણ શ્રેણી મર્યાદિત છે (e = 2 — H).
આ પદ્ધતિ સાથે, ઝડપને મૂળભૂતથી નીચે ગોઠવી શકાય છે, જે ઇલેક્ટ્રોમિકેનિકલ અને મિકેનિકલ લાક્ષણિકતાઓ દ્વારા સાબિત થાય છે. નિયમનની ઉચ્ચ સરળતા સુનિશ્ચિત કરવી મુશ્કેલ છે, કારણ કે નોંધપાત્ર સંખ્યામાં નિયંત્રણ પગલાં અને અનુરૂપ રીતે મોટી સંખ્યામાં સંપર્કકર્તાઓની જરૂર પડશે. આ કિસ્સામાં વર્તમાન (હીટિંગ) માટે મોટરનો સંપૂર્ણ ઉપયોગ સતત લોડ ટોર્ક નિયમન સાથે પ્રાપ્ત થાય છે.
આ પદ્ધતિનો ગેરલાભ એ ગોઠવણ દરમિયાન નોંધપાત્ર પાવર નુકસાનની હાજરી છે, જે કોણીય વેગમાં સંબંધિત ફેરફારના પ્રમાણસર છે. કોણીય વેગ નિયંત્રણની માનવામાં આવતી પદ્ધતિનો ફાયદો એ નિયંત્રણ સર્કિટની સરળતા અને વિશ્વસનીયતા છે.
ઓછી ઝડપે રિઓસ્ટેટમાં ઊંચા નુકસાનને જોતાં, ઝડપ નિયંત્રણની આ પદ્ધતિનો ઉપયોગ ટૂંકા ગાળાના અને તૂટક તૂટક-ટૂંકા ડ્યુટી સાઇકલવાળી ડ્રાઇવ માટે થાય છે.
 બીજી પદ્ધતિમાં, ઉત્તેજના વિન્ડિંગના સર્કિટમાં વધારાના રિઓસ્ટેટની રજૂઆતને કારણે ચુંબકીય પ્રવાહની તીવ્રતા બદલીને સ્વતંત્ર ઉત્તેજનાના ડીસી મોટર્સના કોણીય વેગનું નિયંત્રણ હાથ ધરવામાં આવે છે. જ્યારે પ્રવાહ નબળો પડે છે, ત્યારે લોડ હેઠળ અને નિષ્ક્રિય ઝડપે બંને એન્જિનનો કોણીય વેગ વધે છે, અને જ્યારે પ્રવાહ દર વધે છે, ત્યારે તે ઘટે છે. મોટરના સંતૃપ્તિને કારણે ફક્ત ગતિમાં વધારો કરવો વ્યવહારીક રીતે શક્ય છે.
બીજી પદ્ધતિમાં, ઉત્તેજના વિન્ડિંગના સર્કિટમાં વધારાના રિઓસ્ટેટની રજૂઆતને કારણે ચુંબકીય પ્રવાહની તીવ્રતા બદલીને સ્વતંત્ર ઉત્તેજનાના ડીસી મોટર્સના કોણીય વેગનું નિયંત્રણ હાથ ધરવામાં આવે છે. જ્યારે પ્રવાહ નબળો પડે છે, ત્યારે લોડ હેઠળ અને નિષ્ક્રિય ઝડપે બંને એન્જિનનો કોણીય વેગ વધે છે, અને જ્યારે પ્રવાહ દર વધે છે, ત્યારે તે ઘટે છે. મોટરના સંતૃપ્તિને કારણે ફક્ત ગતિમાં વધારો કરવો વ્યવહારીક રીતે શક્ય છે.
જેમ જેમ પ્રવાહને નબળો પાડીને ઝડપ વધે છે તેમ, ડીસી મોટરનો અનુમતિપાત્ર ટોર્ક હાઇપરબોલા કાયદા અનુસાર બદલાય છે, જ્યારે પાવર સ્થિર રહે છે. આ પદ્ધતિ માટે ઝડપ નિયંત્રણ શ્રેણી e = 2 - 4.
મોટર ફ્લક્સના વિવિધ મૂલ્યો માટેની યાંત્રિક લાક્ષણિકતાઓ ફિગમાં બતાવવામાં આવી છે. 2i અને 2, b, જેમાંથી તે જોઈ શકાય છે કે રેટ કરેલ પ્રવાહની અંદરની લાક્ષણિકતાઓમાં ઉચ્ચ ડિગ્રીની જડતા છે.
સ્વતંત્ર રીતે ઉત્તેજિત ડીસી મોટર્સના ફીલ્ડ વિન્ડિંગ્સમાં નોંધપાત્ર ઇન્ડક્ટન્સ હોય છે. તેથી, ફિલ્ડ વિન્ડિંગ સર્કિટમાં રિઓસ્ટેટના પ્રતિકારમાં એક પગલું ફેરફાર સાથે, વર્તમાન અને તેથી પ્રવાહ ઝડપથી બદલાશે. આ સંદર્ભે, કોણીય વેગ નિયંત્રણ સરળ રીતે કરવામાં આવશે.
આ ઝડપ નિયંત્રણ પદ્ધતિના મુખ્ય ફાયદાઓ તેની સરળતા અને ઉચ્ચ કાર્યક્ષમતા છે.
આ નિયંત્રણ પદ્ધતિનો ઉપયોગ ડ્રાઇવ્સમાં સહાયક તરીકે થાય છે, જે મિકેનિઝમની નિષ્ક્રિય ગતિમાં વધારો પ્રદાન કરે છે.
ગતિને નિયંત્રિત કરવાની ત્રીજી રીત એ છે કે મોટરના આર્મેચર વિન્ડિંગ પર લાગુ થતા વોલ્ટેજને બદલવો.DC મોટરનો કોણીય વેગ, લોડને ધ્યાનમાં લીધા વિના, આર્મેચર પર લાગુ થતા વોલ્ટેજના સીધા પ્રમાણમાં બદલાય છે. તમામ કંટ્રોલ લાક્ષણિકતાઓ કઠોર હોવાથી અને તમામ લાક્ષણિકતાઓ માટે તેમની જડતાની ડિગ્રી યથાવત હોવાથી, મોટર કામગીરી તમામ કોણીય વેગ પર સ્થિર છે અને તેથી લોડને ધ્યાનમાં લીધા વિના ઝડપ નિયંત્રણની વિશાળ શ્રેણી પ્રદાન કરવામાં આવે છે. આ શ્રેણી 10 છે અને વિશેષ નિયંત્રણ યોજનાઓ દ્વારા વિસ્તૃત કરી શકાય છે.
આ પદ્ધતિથી, કોણીય વેગ ઘટાડી શકાય છે અને મૂળભૂત વેગની તુલનામાં વધારી શકાય છે. પ્રવેગક એસી વોલ્ટેજ સ્ત્રોત ક્ષમતાઓ અને મોટરના યુનોમર દ્વારા મર્યાદિત છે.
જો પાવર સ્ત્રોત મોટર પર લાગુ થતા વોલ્ટેજમાં સતત ફેરફાર કરવાની ક્ષમતા પ્રદાન કરે છે, તો મોટર ગતિ નિયંત્રણ સરળ રહેશે.
આ નિયંત્રણ પદ્ધતિ આર્થિક છે કારણ કે સ્વતંત્ર રીતે ઉત્તેજિત ડીસી મોટરનું કોણીય વેગ નિયંત્રણ આર્મેચર સપ્લાય સર્કિટમાં વધારાના પાવર નુકસાન વિના કરવામાં આવે છે. ઉપરોક્ત તમામ સૂચકાંકો માટે, નિયમનની આ પદ્ધતિ પ્રથમ અને બીજાની તુલનામાં શ્રેષ્ઠ છે.