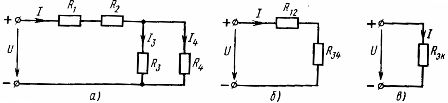
એક જ સપ્લાય સાથે અનબ્રાન્ચ્ડ અને બ્રાન્ચેડ રેખીય વિદ્યુત સર્કિટ

જો e ના સ્ત્રોત સાથે મોટી સંખ્યામાં નિષ્ક્રિય તત્વો હોય. વગેરે c. ઇલેક્ટ્રિક સર્કિટ બનાવે છે, તેમનું ઇન્ટરકનેક્શન જુદી જુદી રીતે કરી શકાય છે. આવા જોડાણો માટે નીચેની લાક્ષણિક યોજનાઓ છે.

તત્વોનું સીરીયલ જોડાણ આ સૌથી સરળ જોડાણ છે. આ જોડાણ સાથે, સર્કિટના તમામ ઘટકોમાં સમાન પ્રવાહ વહે છે. આ યોજના અનુસાર, કાં તો સર્કિટના તમામ નિષ્ક્રિય તત્વોને જોડી શકાય છે, અને પછી સર્કિટ સિંગલ-સર્કિટ અનબ્રાન્ચેડ હશે (ફિગ. 1., એ), અથવા મલ્ટિ-સર્કિટ સર્કિટના ઘટકોનો માત્ર એક ભાગ હોઈ શકે છે. જોડાયેલ

જો n તત્વો શ્રેણીમાં જોડાયેલા હોય જેમાં સમાન પ્રવાહ I વહેતો હોય, તો સર્કિટના ટર્મિનલ્સ પરનો વોલ્ટેજ શ્રેણીમાં જોડાયેલા n તત્વોમાં વોલ્ટેજના ડ્રોપના સરવાળા જેટલો હશે, એટલે કે.

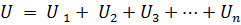
અથવા:

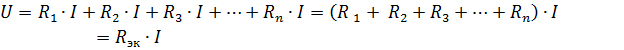
જ્યાં રેક એ સમકક્ષ સર્કિટ પ્રતિકાર છે.

તેથી, શ્રેણીમાં જોડાયેલા નિષ્ક્રિય તત્વોનો સમકક્ષ પ્રતિકાર આ તત્વોના પ્રતિકારના સરવાળા જેટલો છે... વિદ્યુત યોજના (ફિગ.1, a) એક સમકક્ષ સર્કિટ રજૂ કરી શકાય છે (ફિગ. 1, b), જેમાં સમકક્ષ પ્રતિકાર રેક સાથે એક તત્વનો સમાવેશ થાય છે.

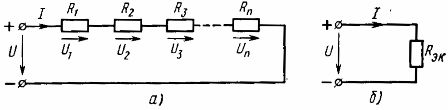
ચોખા. 1. રેખીય તત્વોના સીરીયલ કનેક્શનની યોજના (a) અને તેની સમકક્ષ યોજના (b)

પાવર સ્ત્રોત અને તત્વોના પ્રતિકારના આપેલ વોલ્ટેજ પર શ્રેણીમાં જોડાયેલા તત્વો સાથે સર્કિટની ગણતરી કરતી વખતે, સર્કિટમાં વર્તમાનની ગણતરી ઓહ્મના નિયમ અનુસાર કરવામાં આવે છે:

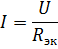
સમગ્ર kth તત્વમાં વોલ્ટેજ ડ્રોપ

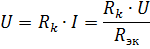
ફક્ત આ તત્વના પ્રતિકાર પર જ નહીં, પણ સમકક્ષ પ્રતિકાર રેક પર પણ આધાર રાખે છે, એટલે કે, સર્કિટના અન્ય ઘટકોના પ્રતિકાર પર. તત્વોના સીરીયલ કનેક્શનનો આ નોંધપાત્ર ગેરલાભ છે. મર્યાદિત કિસ્સામાં, જ્યારે સર્કિટના કોઈપણ તત્વનો પ્રતિકાર અનંત (ઓપન સર્કિટ) ની સમાન બને છે, ત્યારે સર્કિટના તમામ ઘટકોમાં વર્તમાન શૂન્ય બની જાય છે.

કારણ કે, જ્યારે શ્રેણીમાં જોડાયેલ હોય, ત્યારે સર્કિટના તમામ ઘટકોમાં વર્તમાન સમાન હોય છે, તત્વોમાં વોલ્ટેજ ડ્રોપનો ગુણોત્તર આ તત્વોના પ્રતિકારના ગુણોત્તર જેટલો હોય છે:

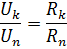
તત્વોનું સમાંતર જોડાણ - આ એક જોડાણ છે જેમાં સર્કિટના તમામ ઘટકો પર સમાન વોલ્ટેજ લાગુ કરવામાં આવે છે. સમાંતર જોડાણ યોજના અનુસાર, કાં તો સર્કિટના તમામ નિષ્ક્રિય તત્વો (ફિગ. 2, એ) અથવા તેનો માત્ર એક ભાગ જ કનેક્ટ કરી શકાય છે. દરેક સમાંતર જોડાયેલ તત્વ એક અલગ શાખા બનાવે છે. તેથી, ફિગમાં બતાવેલ તત્વોના સમાંતર જોડાણ સાથેનું સર્કિટ. 2, a, જો કે તે એક સરળ સર્કિટ છે (કારણ કે તેમાં ફક્ત બે ગાંઠો છે), તે એક જ સમયે ડાળીઓવાળું છે.

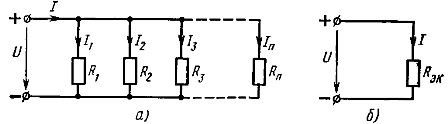
ચોખા. 2. રેખીય તત્વોના સમાંતર જોડાણની યોજના (a) અને તેની સમકક્ષ યોજના (b)

દરેક સમાંતર શાખામાં, વર્તમાન

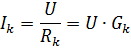
જ્યાં Gk એ kth શાખાની વાહકતા છે.

થી કિર્ચહોફનો પ્રથમ કાયદો

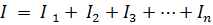
અથવા

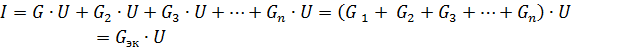
જ્યાં Gec એ સમકક્ષ સર્કિટ વહન છે.

તેથી, જ્યારે નિષ્ક્રિય તત્વો સમાંતર રીતે જોડાયેલા હોય છે, ત્યારે તેમની સમકક્ષ વાહકતા આ તત્વોના વાહકતાના સરવાળા જેટલી હોય છે... સમકક્ષ વાહકતા હંમેશા સમાંતર શાખાઓના કોઈપણ ભાગના વહન કરતા વધારે હોય છે. સમકક્ષ વાહકતા GEK સમકક્ષ પ્રતિકાર Rek = 1 / Gek ને અનુલક્ષે છે.

પછી ફિગમાં બતાવેલ સમકક્ષ સર્કિટ. 2, a, અંજીરમાં બતાવેલ ફોર્મ હશે. 2, b. તત્વોના સમાંતર જોડાણ સાથે સર્કિટના અબ્રાન્ચેડ ભાગમાં પ્રવાહ આ સર્કિટમાંથી ઓહ્મના નિયમ અનુસાર નક્કી કરી શકાય છે:

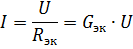
તેથી, જો સપ્લાય વોલ્ટેજ સતત હોય, તો પછી સમાંતરમાં જોડાયેલા તત્વોની સંખ્યામાં વધારા સાથે (જે સમકક્ષ વાહકતામાં વધારો તરફ દોરી જાય છે), સર્કિટના અબ્રાન્ચેડ ભાગમાં વર્તમાન (વીજ પુરવઠો વર્તમાન) વધે છે.

સૂત્રમાંથી

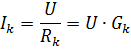
તે જોઈ શકાય છે કે દરેક શાખામાં પ્રવાહ ફક્ત તે શાખાના વહન પર આધાર રાખે છે અને અન્ય શાખાઓના વહન પર આધારિત નથી. એકબીજાથી સમાંતર શાખા સ્થિતિઓની સ્વતંત્રતા એ નિષ્ક્રિય તત્વોના સમાંતર જોડાણનો એક મહત્વપૂર્ણ ફાયદો છે. ઔદ્યોગિક સ્થાપનોમાં, મોટાભાગના કિસ્સાઓમાં ઇલેક્ટ્રિકલ રીસીવરોના સમાંતર જોડાણનો ઉપયોગ થાય છે. સૌથી સ્પષ્ટ ઉદાહરણ લાઇટિંગ માટે ઇલેક્ટ્રિક લેમ્પ્સનો સમાવેશ છે.

સમાંતર જોડાણમાં બધા તત્વો પર સમાન વોલ્ટેજ લાગુ પડતો હોવાથી અને દરેક શાખામાંનો પ્રવાહ તે શાખાના વહનના પ્રમાણમાં હોય છે, તેથી સમાંતર શાખાઓમાં પ્રવાહોનો ગુણોત્તર આ શાખાઓના વાહકતાના ગુણોત્તર જેટલો હોય છે, અથવા વિપરિત પ્રમાણસર હોય છે. તેમના પ્રતિકારના ગુણોત્તરમાં:

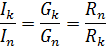
તત્વોનું મિશ્ર જોડાણ એ શ્રેણી અને સમાંતર જોડાણોનું સંયોજન છે. આવી સાંકળમાં વિવિધ ગાંઠો અને શાખાઓ હોઈ શકે છે. મિશ્ર જોડાણનું ઉદાહરણ ડાયાગ્રામમાં બતાવવામાં આવ્યું છે (ફિગ. 3, a)

ચોખા. 3. રેખીય તત્વો (a) અને તેની સમકક્ષ યોજનાઓ (b, c) ના મિશ્ર જોડાણની યોજના.

આવા સર્કિટની ગણતરી કરવા માટે, સર્કિટના તે ભાગો માટે સમાન પ્રતિકાર ક્રમિક રીતે નિર્ધારિત કરવા જરૂરી છે જે ફક્ત શ્રેણી અથવા માત્ર સમાંતર જોડાણ છે. માનવામાં આવેલ સર્કિટમાં, પ્રતિકાર R1 અને R2 સાથે તત્વોનું શ્રેણીબદ્ધ જોડાણ અને પ્રતિકાર R3 અને R4 સાથે તત્વોનું સમાંતર જોડાણ છે. તેમની શ્રેણી અને સમાંતર જોડાણ સાથે સર્કિટ તત્વોના પરિમાણો વચ્ચે અગાઉ મેળવેલા સંબંધોનો ઉપયોગ કરીને, વાસ્તવિક વિદ્યુત સર્કિટને અનુક્રમે સમકક્ષ સર્કિટ દ્વારા બદલી શકાય છે.

શ્રેણીમાં જોડાયેલા તત્વોનો સમકક્ષ પ્રતિકાર

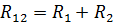
સમાંતર જોડાયેલા તત્વો R3 અને R4 નો સમકક્ષ પ્રતિકાર

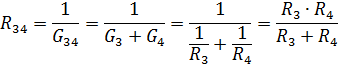
તત્વો R12 અને R34 ના પ્રતિકાર સાથે સમકક્ષ સર્કિટ ફિગમાં બતાવવામાં આવે છે. 3, બી. R12 અને R34 ના આ શ્રેણી જોડાણ માટે, સમકક્ષ પ્રતિકાર છે

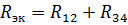
અને અનુરૂપ સમકક્ષ સર્કિટ ફિગમાં બતાવેલ છે. 2, બી. ચાલો આ સર્કિટમાં વર્તમાન શોધીએ:

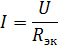
વાસ્તવિક સર્કિટના R1 અને R2 તત્વોમાં આ પુરવઠા વર્તમાન અને વર્તમાન છે.I3 અને I4 પ્રવાહોની ગણતરી કરવા માટે, પ્રતિકાર R34 (ફિગ. 3, b) સાથે સર્કિટના વિભાગમાં વોલ્ટેજ નક્કી કરો:

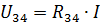
પછી પ્રવાહ I3 અને I4 ઓહ્મના નિયમ અનુસાર શોધી શકાય છે:

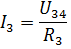
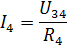
એ જ રીતે, તમે નિષ્ક્રિય તત્વોના મિશ્ર જોડાણ સાથે સંખ્યાબંધ અન્ય વિદ્યુત સર્કિટની ગણતરી કરી શકો છો.

મોટી સંખ્યામાં સર્કિટ અને સ્ત્રોતો સાથે જટિલ સર્કિટ માટે ઇ. વગેરે c. આવા સમકક્ષ રૂપાંતરણ હંમેશા હાથ ધરી શકાતું નથી. તેઓ અન્ય પદ્ધતિઓ દ્વારા ગણવામાં આવે છે.