ચુંબકીય સર્કિટ માટે ઓહ્મનો નિયમ

જો ત્યાં કોઈ ચુંબકીય પ્રવાહ ન હોત, તો તે અસંભવિત છે કે આધુનિક ઇલેક્ટ્રિકલ એન્જિનિયરિંગ અસ્તિત્વમાં હોત. જનરેટર અને ઇલેક્ટ્રિક મોટર્સ, ઇલેક્ટ્રોમેગ્નેટ અને ટ્રાન્સફોર્મર્સ, માપવાના સાધનો અને હોલ સેન્સર્સનું સંચાલન ચુંબકીય ક્ષેત્રના ઉપયોગ અને ચુંબકીય પ્રવાહના ગુણધર્મો પર આધારિત છે.

ચુંબકીય પ્રવાહને કેન્દ્રિત અને મજબૂત કરવા માટે, તેઓ લોહચુંબકીય સામગ્રીનો ઉપયોગ કરે છે. ફેરોમેગ્નેટિક સામગ્રીઓ ઉત્પન્ન થાય છે ચુંબકીય કોરો - જરૂરી આકારો અને કદના શરીર, એક અથવા બીજા કદના ચુંબકીય પ્રવાહોને જરૂરી દિશામાં દિશામાન કરવા માટેના કોરો. આવા શરીર, જેની અંદર ચુંબકીય ઇન્ડક્શનની બંધ રેખાઓ પસાર થાય છે, તેને ચુંબકીય સર્કિટ કહેવામાં આવે છે.

ચુંબકીય ક્ષેત્રના જાણીતા ગુણધર્મો વિવિધ ચુંબકીય સર્કિટમાં ચુંબકીય પ્રવાહની ગણતરી કરવાનું શક્ય બનાવે છે. પરંતુ વ્યવહારુ કાર્ય માટે, દરેક વખતે આ કાયદાઓનો સીધો ઉપયોગ કરવાને બદલે, ચુંબકીય ક્ષેત્રના કાયદાઓમાંથી મેળવેલા ચુંબકીય સર્કિટના સામાન્ય પરિણામો અને કાયદાઓનો આશરો લેવો વધુ અનુકૂળ છે. ચુંબકીય સર્કિટ્સ પર અમુક નિયમો લાગુ કરવા એ લાક્ષણિક વ્યવહારિક સમસ્યાઓ ઉકેલવા માટે વધુ અનુકૂળ છે.

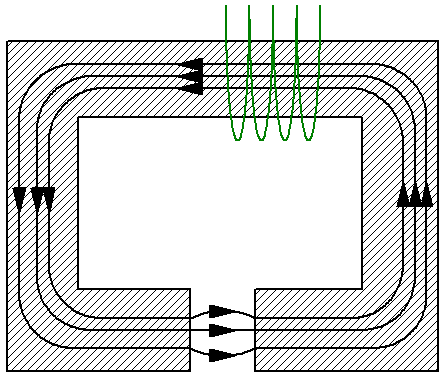
ઉદાહરણ તરીકે, એક સરળ ચુંબકીય સર્કિટનો વિચાર કરો કે જેમાં ક્રોસ-સેક્શન S ના અનબ્રાન્ચ્ડ યોકનો સમાવેશ થાય છે, જે બદલામાં સામગ્રીથી બનેલો છે અભેદ્યતા mu… યોકમાં સમાન વિસ્તાર S નો બિન-ચુંબકીય અંતર છે, ઉદાહરણ તરીકે હવા, અને ગેપમાં ચુંબકીય અભેદ્યતા — mu1 — યોકની ચુંબકીય અભેદ્યતાથી અલગ છે. અહીં તમે ઇન્ડક્શનની સરેરાશ રેખા જોઈ શકો છો અને તેના પર ચુંબકીય તણાવ પ્રમેય લાગુ કરી શકો છો:

સમગ્ર સર્કિટમાં ચુંબકીય ઇન્ડક્શનની રેખાઓ સતત હોવાથી, યોક અને ગેપ બંનેમાં ચુંબકીય પ્રવાહની તીવ્રતા સમાન છે. હવે આપણે માટે સૂત્રોનો ઉપયોગ કરીએ છીએ ચુંબકીય ઇન્ડક્શન B અને ચુંબકીય પ્રવાહ F માટે ચુંબકીય ક્ષેત્રની તાકાત H દર્શાવવા માટે ચુંબકીય પ્રવાહ F ની દ્રષ્ટિએ.

આગળનું પગલું એ ચુંબકીય પ્રવાહ પ્રમેયના ઉપરના સૂત્રમાં પરિણામી અભિવ્યક્તિઓને બદલવાનું છે:

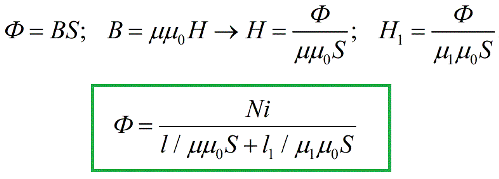
અમે વિદ્યુત ઇજનેરીમાં જાણીતા ફોર્મ્યુલા જેવું જ એક સૂત્ર મેળવ્યું છે બંધ સર્કિટના વિભાગ માટે ઓહ્મનો કાયદો, અને અહીં EMF ની ભૂમિકા iN ના જથ્થા દ્વારા ભજવવામાં આવે છે, જેને ઇલેક્ટ્રોમોટિવ બળ સાથે સામ્યતા દ્વારા મેગ્નેટોમોટિવ ફોર્સ (અથવા MDF) કહેવાય છે. SI સિસ્ટમમાં, મેગ્નેટોમોટિવ ફોર્સ એમ્પીયરમાં માપવામાં આવે છે.

છેદમાંનો સરવાળો એ ઇલેક્ટ્રિક સર્કિટ માટેના કુલ વિદ્યુત પ્રતિકારની સામ્યતા કરતાં વધુ કંઈ નથી, અને ચુંબકીય સર્કિટ માટે તેને તે મુજબ કુલ ચુંબકીય પ્રતિકાર કહેવામાં આવે છે. છેદમાંના શબ્દો ચુંબકીય સર્કિટના વ્યક્તિગત વિભાગોના ચુંબકીય પ્રતિકાર છે.

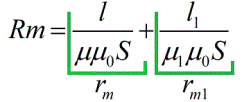
ચુંબકીય પ્રતિકાર ચુંબકીય સર્કિટની લંબાઈ, તેના ક્રોસ-વિભાગીય વિસ્તાર અને ચુંબકીય અભેદ્યતા (સામાન્ય ઓહ્મના નિયમ માટે વિદ્યુત વાહકતા સમાન) પર આધાર રાખે છે.પરિણામે, તમે માત્ર ચુંબકીય સર્કિટ માટે ઓહ્મના નિયમનું સૂત્ર લખી શકો છો:

એટલે કે, ચુંબકીય સર્કિટના સંબંધમાં ઓહ્મના કાયદાની રચના આના જેવી લાગે છે: "શાખા વગરના ચુંબકીય સર્કિટમાં, ચુંબકીય પ્રવાહ સર્કિટના કુલ ચુંબકીય પ્રતિકાર દ્વારા MDS ના વિભાજનના ભાગની બરાબર છે."

તે સૂત્રો પરથી સ્પષ્ટ છે કે ચુંબકીય પ્રતિકાર NE માં વેબર એમ્પીયરમાં માપવામાં આવે છે, અને ચુંબકીય સર્કિટનો કુલ ચુંબકીય પ્રતિકાર સંખ્યાત્મક રીતે તે ચુંબકીય સર્કિટના ભાગોના ચુંબકીય પ્રતિકારના સરવાળા જેટલો છે.

વર્ણવેલ પરિસ્થિતિ એક શાખા વિનાના ચુંબકીય સર્કિટ માટે માન્ય છે જેમાં કોઈપણ સંખ્યાબંધ ભાગોનો સમાવેશ થાય છે, જો કે ચુંબકીય પ્રવાહ ક્રમિક રીતે આ તમામ ભાગોમાં પ્રવેશ કરે. જો ચુંબકીય કોરો શ્રેણીમાં જોડાયેલા હોય, તો ભાગોના ચુંબકીય પ્રતિકારને ઉમેરીને કુલ ચુંબકીય પ્રતિકાર જોવા મળે છે.

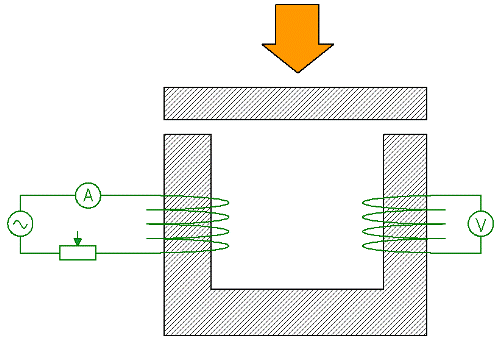
હવે એક પ્રયોગનો વિચાર કરો જે સર્કિટની કુલ અનિચ્છા પર સર્કિટના ભાગોની અનિચ્છાની અસર દર્શાવે છે. એક U-આકારનું ચુંબકીય સર્કિટ કોઇલ 1 દ્વારા ચુંબકીય કરવામાં આવે છે, જેને એમીટર અને રિઓસ્ટેટ દ્વારા ખવડાવવામાં આવે છે (વૈકલ્પિક પ્રવાહ). સેકન્ડરી વિન્ડિંગ 2 માં EMF પ્રેરિત થાય છે, અને વિન્ડિંગ સાથે જોડાયેલા વોલ્ટમીટરના રીડિંગ્સ, જેમ તમે જાણો છો, ચુંબકીય સર્કિટમાં ચુંબકીય પ્રવાહના પ્રમાણસર છે.

જો તમે હવે પ્રાથમિક વિન્ડિંગમાં વર્તમાનને રિઓસ્ટેટ વડે નિયમન કરીને યથાવત રાખશો, અને તે જ સમયે ઉપરના ચુંબકીય સર્કિટની સામે લોખંડની પ્લેટને દબાવો, તો સર્કિટનો કુલ ચુંબકીય પ્રતિકાર ઘણો ઓછો થઈ જશે પછી, તેનું વાંચન વોલ્ટમીટર તે મુજબ વધશે.

અલબત્ત, ઉપરોક્ત શબ્દો, જેમ કે "મેગ્નેટોરેસિસ્ટન્સ" અને "મેગ્નેટોમોટિવ ફોર્સ", ઔપચારિક ખ્યાલો છે, કારણ કે ચુંબકીય પ્રવાહમાં કંઈપણ ચાલતું નથી, ત્યાં કોઈ ગતિશીલ કણો નથી, તે માત્ર દ્રશ્ય રજૂઆત છે (જેમ કે પ્રવાહી પ્રવાહ મોડેલ) કાયદાઓની સ્પષ્ટ સમજ...

ઉપરોક્ત પ્રયોગ અને અન્ય સમાન પ્રયોગોનો ભૌતિક અર્થ એ સમજવાનો છે કે ચુંબકીય સર્કિટમાં બિન-ચુંબકીય ગાબડાં અને ચુંબકીય પદાર્થોનો પરિચય ચુંબકીય સર્કિટમાં ચુંબકીય પ્રવાહને કેવી રીતે અસર કરે છે.

દાખલા તરીકે, ચુંબકીય સર્કિટમાં ચુંબક દાખલ કરીને, અમે સર્કિટમાં પહેલેથી જ સમાવિષ્ટ શરીરમાં વધારાના મોલેક્યુલર પ્રવાહો ઉમેરીએ છીએ, જે વધારાના ચુંબકીય પ્રવાહનો પરિચય આપે છે. ઔપચારિક વિભાવનાઓ જેમ કે "ચુંબકીય પ્રતિકાર" અને "મેગ્નેટોમોટિવ ફોર્સ" વ્યવહારિક સમસ્યા હલ કરતી વખતે ખૂબ જ અનુકૂળ સાબિત થાય છે, તેથી જ તેનો ઇલેક્ટ્રિકલ એન્જિનિયરિંગમાં સફળતાપૂર્વક ઉપયોગ થાય છે.