સર્કિટ ટોપોલોજીસ-મૂળભૂત ખ્યાલો

ઇલેક્ટ્રિકલ સર્કિટ એ ઉપકરણો (તત્વો) અને તેમના કનેક્ટિંગ વાયરનો સમૂહ છે જેના દ્વારા ઇલેક્ટ્રિક પ્રવાહ વહે છે. ઇલેક્ટ્રિક સર્કિટના તમામ ઘટકો શેર કરે છે નિષ્ક્રિય અને સક્રિય માં.

સક્રિય તત્વો વિવિધ પ્રકારની ઊર્જા (યાંત્રિક, રાસાયણિક, પ્રકાશ, વગેરે)ને વિદ્યુત ઊર્જામાં રૂપાંતરિત કરે છે. નિષ્ક્રિય ઉપકરણોમાં, વિદ્યુત ઊર્જા અન્ય પ્રકારની ઊર્જામાં રૂપાંતરિત થાય છે. સક્રિય તત્વોને સ્ત્રોત કહેવામાં આવે છે, નિષ્ક્રિય તત્વોને ઉપભોક્તા અથવા રીસીવર કહેવામાં આવે છે.

સર્કિટ થિયરીમાં, વિદ્યુત તત્વોના આદર્શ મોડેલો ગણવામાં આવે છે. આ તત્વોનું વર્ણન શક્ય તેટલું સરળ બનાવે છે. વધુ જટિલ, વાસ્તવિક તત્વો આદર્શ તત્વોના સમૂહમાંથી બનાવવામાં આવે છે.

ઇલેક્ટ્રિક સર્કિટના મુખ્ય નિષ્ક્રિય તત્વો રેઝિસ્ટર (પ્રતિરોધક તત્વ), ઇન્ડક્ટર (ઇન્ડેક્ટિવ એલિમેન્ટ) અને કેપેસિટર (કેપેસિટીવ એલિમેન્ટ) છે. આપેલ મૂલ્ય અને આકારના વોલ્ટેજ અને વર્તમાન પેદા કરવા માટે તત્વો ઇલેક્ટ્રિક સર્કિટમાં સ્થાપિત થાય છે (જુઓ — ઇલેક્ટ્રિક સર્કિટ અને તેના તત્વો).

ઇલેક્ટ્રિકલ સર્કિટમાં શાખાઓ અને ગાંઠો હોય છે. શાખા - આ ઇલેક્ટ્રિકલ સર્કિટ (સર્કિટ) નો એક વિભાગ છે જેના દ્વારા સમાન પ્રવાહ વહે છે. એક ગાંઠ - ત્રણ અથવા વધુ શાખાઓનું જોડાણ. વિદ્યુત રેખાકૃતિ પર, નોડ એક બિંદુ (ફિગ. 1) દ્વારા સૂચવવામાં આવે છે.

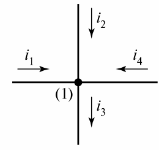
ચોખા. 1. આકૃતિમાં નોડ વ્યાખ્યાયિત કરો

જો જરૂરી હોય તો, ડાયાગ્રામના ગાંઠોને ડાબેથી જમણે ઉપરથી નીચે સુધી ક્રમાંકિત કરવામાં આવે છે.

અંજીરમાં. 2 એ રેઝિસ્ટિવ-કેપેસિટીવ શાખા બતાવે છે જેમાં વર્તમાન iC વહે છે.

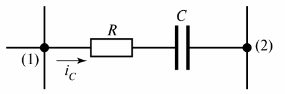
ચોખા. 2. પ્રતિકારક-કેપેસિટીવ શાખા

શાખાની બીજી વ્યાખ્યા આપી શકાય છે - તે બે અડીને આવેલા ગાંઠો (નોડ્સ (1) અને (2) ફિગ. 2 વચ્ચેના સર્કિટનો વિભાગ છે).

સાંકળ શું ઇલેક્ટ્રિકલ સર્કિટમાં કોઈ બંધ પાથ છે. સર્કિટ કોઈપણ શાખાઓ દ્વારા બંધ કરી શકાય છે, જેમાં શરતી શાખાઓનો સમાવેશ થાય છે જેની પ્રતિકાર અનંતતા જેટલી હોય છે.

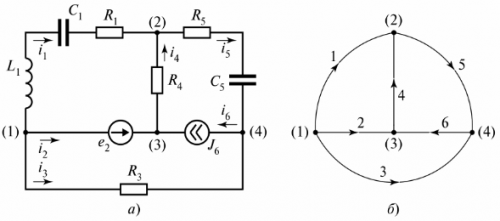
અંજીરમાં. 3 એક શાખાવાળું ઇલેક્ટ્રિકલ સર્કિટ દર્શાવે છે જેમાં ત્રણ શાખાઓ હોય છે.

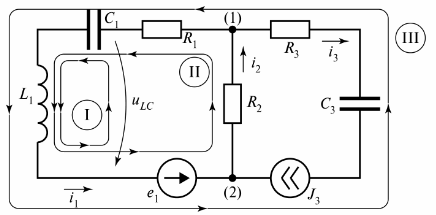
ચોખા. 3. બે સર્કિટ સાથે ઇલેક્ટ્રિક સર્કિટ

આકૃતિ ત્રણ સર્કિટ બતાવે છે, અને સર્કિટ I અનંત પ્રતિકારની શાખા દ્વારા બંધ છે. આ શાખા વોલ્ટેજ tiLC તરીકે દર્શાવવામાં આવે છે.

ફિગ ના સર્કિટ માટે. 3 વાસ્તવિક અથવા શરતી શાખાઓ દ્વારા બંધ કરાયેલા ઘણા લૂપ્સ કંપોઝ કરવાનું શક્ય છે, પરંતુ વિદ્યુત અવાજની ગણતરી માટે "સ્વતંત્ર લૂપ" ની વિભાવનાનો ઉપયોગ થાય છે. સ્વતંત્ર સર્કિટ લૂપ્સની સંખ્યા હંમેશા ગણતરી માટે જરૂરી ન્યૂનતમ તરીકે સેટ કરવામાં આવે છે.

સ્વતંત્ર સર્કિટ હંમેશા બંધ હોય છે, પરંતુ જે શાખાઓ અનંતની સમાન ન હોય તેવી પ્રતિકારકતા ધરાવે છે અને દરેક સ્વતંત્ર સર્કિટમાં ઓછામાં ઓછી એક શાખાનો સમાવેશ થાય છે જે અન્ય સર્કિટમાં સમાવિષ્ટ નથી. જટિલ વિદ્યુત સર્કિટ માટે, તમે સર્કિટ ડાયાગ્રામનો ઉપયોગ કરીને સ્વતંત્ર સર્કિટની સંખ્યા નક્કી કરી શકો છો.

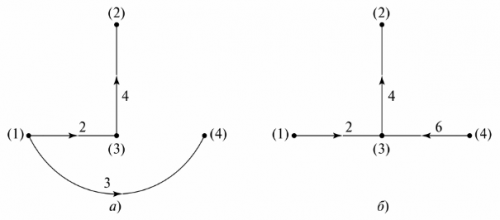
સર્કિટ ડાયાગ્રામ પર સર્કિટની શરતી રજૂઆત કહેવામાં આવે છે, જેમાં દરેક શાખાને લાઇન સેગમેન્ટ દ્વારા બદલવામાં આવે છે. શાખાઓમાં વસ્તુઓ પ્રદર્શિત થતી નથી. ઉદાહરણ તરીકે, FIG માં. 4 એક શાખા સર્કિટ અને તેની રેખાકૃતિ દર્શાવે છે.

ચોખા. 4. બ્રાન્ચ્ડ ઇલેક્ટ્રિક સર્કિટ: a — સર્કિટ ડાયાગ્રામ, b — ડાયાગ્રામ

ડાયાગ્રામની આકૃતિ બનાવવા માટે, તમારે ગાંઠોને તેમના પર તત્વોનો ઉલ્લેખ કર્યા વિના શાખા રેખાઓ સાથે કનેક્ટ કરવું આવશ્યક છે. શાખાઓ ક્રમાંકિત છે, અને તેમના પરના પ્રવાહોની દિશાઓ તીર દ્વારા સૂચવવામાં આવે છે. ગ્રાફનો પોતે કોઈ ભૌતિક અર્થ નથી, પરંતુ તેનો ઉપયોગ સ્વતંત્ર રૂપરેખાની સંખ્યા અને પ્રકાર નક્કી કરવા માટે થઈ શકે છે. આ હેતુ માટે, "ગ્રાફિક વૃક્ષ" તૈયાર કરવામાં આવે છે.

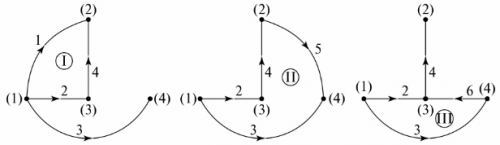
ગ્રાફિક વૃક્ષ તે સર્કિટના ગ્રાફને રજૂ કરે છે જેના ગાંઠો શાખાઓ દ્વારા એવી રીતે જોડાયેલા હોય છે કે કોઈ બંધ લૂપ પરિણામ ન આવે. ગ્રાફિકલ ટ્રી દર્શાવવા માટે ઘણા વિકલ્પો હોઈ શકે છે. અંજીરમાં. 5 FIG ના સર્કિટ માટે બે સંભવિત વિકલ્પો બતાવે છે. 4.

ચોખા. 5. યોજનાનું ગ્રાફિક વૃક્ષ

ગ્રાફ ટ્રીમાં ગુમ થયેલ શાખાઓની સંખ્યા સર્કિટના સ્વતંત્ર લૂપ્સની સંખ્યા જેટલી છે. ઉદાહરણમાં, આ ત્રણ શાખાઓ, ત્રણ સ્વતંત્ર લૂપ્સ છે. સ્વતંત્ર લૂપ્સનું રૂપરેખાંકન અનુક્રમે ગ્રાફ ટ્રીના નોડ્સને શાખાઓ સાથે જોડીને મેળવી શકાય છે જે ગ્રાફ ટ્રી પર નિર્દિષ્ટ નથી. ઉદાહરણ તરીકે, ફિગમાં ગ્રાફ ટ્રી માટે. 5, અને સ્વતંત્ર રૂપરેખા ફિગમાં બતાવવામાં આવી છે. 6.

ચોખા. 6. ગ્રાફ ટ્રી દ્વારા સ્વતંત્ર રૂપરેખા નક્કી કરવી

સર્કિટની ગણતરી કરવા માટે સ્વતંત્ર સર્કિટને ગોઠવવાના વિકલ્પની પસંદગી સર્કિટ વિશ્લેષણ દરમિયાન હાથ ધરવામાં આવે છે. તમારે આવા રૂપરેખા પસંદ કરવા જોઈએ જેથી ગણતરી શક્ય તેટલી સરળ હોય, એટલે કે. સિસ્ટમમાં નિર્ભર સમીકરણોની સંખ્યા ન્યૂનતમ છે.

ટોપોલોજીકલ સમીકરણો સર્કિટમાં વોલ્ટેજ અને પ્રવાહો વચ્ચે સંબંધ સ્થાપિત કરે છે, અને સમીકરણોની સંખ્યા અને પ્રકાર શાખાઓમાં કયા તત્વોનો સમાવેશ થાય છે તેના પર નિર્ભર નથી. ટોપોલોજીકલ સમીકરણોમાં બનેલા સમીકરણોનો સમાવેશ થાય છે કિર્ચહોફના કાયદા અનુસાર.