મેગ્નેટોમોટિવ ફોર્સ શું છે, હોપકિન્સનનો કાયદો

19મી સદીના ઉત્તરાર્ધમાં, અંગ્રેજ ભૌતિકશાસ્ત્રી જ્હોન હોપકિન્સન અને તેમના ભાઈ એડવર્ડ હોપકિન્સન, ચુંબકીય સર્કિટનો સામાન્ય સિદ્ધાંત વિકસાવતા, "હોપકિન્સનનું સૂત્ર" અથવા હોપકિન્સનનો કાયદો નામનું ગાણિતિક સૂત્ર મેળવ્યું, જે ઓહ્મના કાયદાનું અનુરૂપ છે ઇલેક્ટ્રિકલ સર્કિટની ગણતરી કરવા માટે).

તેથી, જો ઓહ્મનો શાસ્ત્રીય કાયદો ગાણિતિક રીતે વર્તમાન અને ઇલેક્ટ્રોમોટિવ ફોર્સ (EMF) વચ્ચેના સંબંધનું વર્ણન કરે છે, તો હોપકિન્સનનો કાયદો એ જ રીતે ચુંબકીય પ્રવાહ અને કહેવાતા વચ્ચેના સંબંધને વ્યક્ત કરે છે. મેગ્નેટોમોટિવ ફોર્સ (MDF).

પરિણામે, તે બહાર આવ્યું છે મેગ્નેટોમોટિવ ફોર્સ એ ભૌતિક જથ્થા છે જે ચુંબકીય પ્રવાહ બનાવવા માટે ઇલેક્ટ્રિક પ્રવાહોની ક્ષમતાને દર્શાવે છે. અને આ સંદર્ભે હોપકિન્સનનો કાયદો ચુંબકીય સર્કિટની ગણતરીમાં સફળતાપૂર્વક ઉપયોગ કરી શકાય છે, કારણ કે ચુંબકીય સર્કિટમાં MDF ઇલેક્ટ્રિક સર્કિટ્સમાં EMF સાથે સમાન છે. હોપકિન્સનના કાયદાની શોધની તારીખ 1886 માનવામાં આવે છે.

મેગ્નેટોમોટિવ ફોર્સ (MDF) ની તીવ્રતા શરૂઆતમાં એમ્પીયરમાં માપવામાં આવે છે અથવા, જો આપણે વર્તમાન અથવા ઇલેક્ટ્રોમેગ્નેટ સાથે કોઇલ વિશે વાત કરી રહ્યા છીએ, તો ગણતરીની સુવિધા માટે એમ્પીયર-ટર્ન્સમાં તેની અભિવ્યક્તિનો ઉપયોગ કરો:

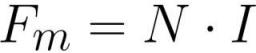
જ્યાં: Fm એ કોઇલ [એમ્પીયર * ટર્ન] માં ચુંબકીય બળ છે, N એ કોઇલ [ટર્ન] માં વળાંકોની સંખ્યા છે, I કોઇલ [એમ્પીયર] ના દરેક વળાંકમાં વર્તમાનનો જથ્થો છે.

જો તમે અહીં ચુંબકીય પ્રવાહ મૂલ્ય દાખલ કરો છો, તો ચુંબકીય સર્કિટ માટે હોપકિન્સનનો કાયદો આ સ્વરૂપ લેશે:

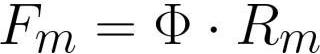
જ્યાં: Fm એ કોઇલ [એમ્પીયર * ટર્ન] માં ચુંબકીય બળ છે, F એ ચુંબકીય પ્રવાહ [વેબર] અથવા [હેનરી * એમ્પીયર] છે, આરએમ એ ચુંબકીય પ્રવાહ વાહક [એમ્પીયર * ટર્ન / વેબર] અથવા [એમ્પીયર * ટર્ન / વેબર] નું ચુંબકીય પ્રતિકાર છે ટર્ન / હેનરી].

હોપકિન્સનના કાયદાનું શાબ્દિક ફોર્મ્યુલેશન મૂળ રૂપે નીચે મુજબ હતું: "અનશાખા વગરના ચુંબકીય સર્કિટમાં, ચુંબકીય પ્રવાહ ચુંબકીય બળના સીધા પ્રમાણસર હોય છે અને કુલ ચુંબકીય પ્રતિકારના વિપરિત પ્રમાણસર હોય છે." એટલે કે, આ કાયદો સર્કિટમાં મેગ્નેટોમોટિવ બળ, અનિચ્છા અને ચુંબકીય પ્રવાહ વચ્ચેનો સંબંધ નક્કી કરે છે:

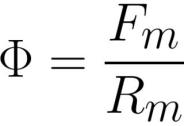
અહીં: F એ ચુંબકીય પ્રવાહ [વેબર] અથવા [હેનરી * એમ્પીયર] છે, એફએમ એ કોઇલ [એમ્પીયર * ક્રાંતિ] માં ચુંબકીય ચુંબકીય બળ છે, Rm એ ચુંબકીય પ્રવાહ વાહક [એમ્પીયર * ક્રાંતિ / વેબર] અથવા [ ટર્ન / હેનરી].

અહીં એ નોંધવું અગત્યનું છે કે વાસ્તવમાં મેગ્નેટોમોટિવ ફોર્સ (MDF) એ ઇલેક્ટ્રોમોટિવ ફોર્સ (EMF) થી મૂળભૂત તફાવત ધરાવે છે, જેમાં એ હકીકતનો સમાવેશ થાય છે કે ચુંબકીય પ્રવાહમાં કોઈ પણ કણો સીધા આગળ વધતા નથી, જ્યારે તેની ક્રિયા હેઠળ ઉદ્ભવતા વર્તમાન EMF ચાર્જ્ડ કણોની હિલચાલ લે છે, ઉદાહરણ તરીકે મેટલ વાયરમાં ઇલેક્ટ્રોન. જો કે, MDS નો વિચાર ચુંબકીય સર્કિટની ગણતરીની સમસ્યાઓ હલ કરવામાં મદદ કરે છે.

ઉદાહરણ તરીકે, એક અબ્રાન્ચેડ ચુંબકીય સર્કિટનો વિચાર કરો જેમાં ક્રોસ-સેક્શનલ એરિયા Sનું યોક શામેલ હોય છે, જે તેની સમગ્ર લંબાઈમાં સમાન હોય છે અને યોકની સામગ્રીમાં ચુંબકીય અભેદ્યતા mu હોય છે.

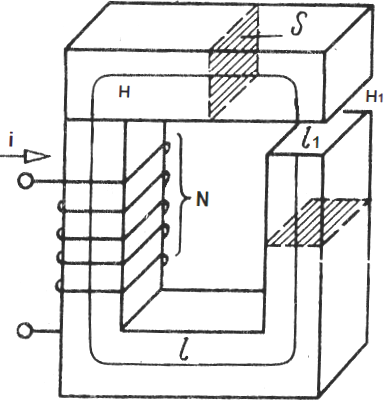
યોકમાં ગેપ - વિવિધ સામગ્રી, ચુંબકીય અભેદ્યતા જે mu1. યોક પર મૂકવામાં આવેલ કોઇલમાં N વળાંકો હોય છે, કોઇલના દરેક વળાંકમાંથી એક કરંટ i વહે છે. અમે યોકની મધ્યરેખા પર ચુંબકીય ક્ષેત્ર પરિભ્રમણ પ્રમેય લાગુ કરીએ છીએ:

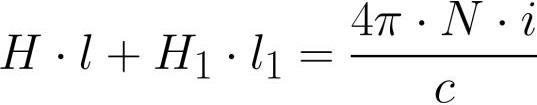
જ્યાં: યોકની અંદર H એ ચુંબકીય ક્ષેત્રની શક્તિ છે, H1 એ ગેપની અંદર ચુંબકીય ક્ષેત્રની તાકાત છે, l એ યોક ઇન્ડક્શનની મધ્યરેખા લંબાઈ છે (ગેપ વિના), l1 એ ગેપની લંબાઈ છે.

યોકની અંદર અને ગેપની અંદરના ચુંબકીય પ્રવાહનું મૂલ્ય સમાન હોવાથી (ચુંબકીય ઇન્ડક્શન રેખાઓની સાતત્યતાને કારણે), Ф = BS અને В = mu * H લખ્યા પછી, અમે ચુંબકીય ક્ષેત્રની મજબૂતાઈને વધુ વિગતવાર લખીશું. , અને પછી આને ઉપરના સૂત્રમાં બદલો:

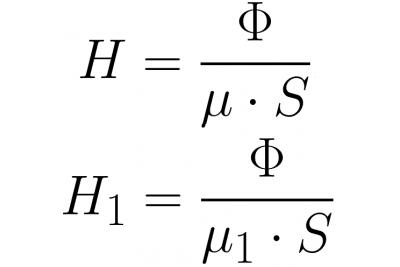
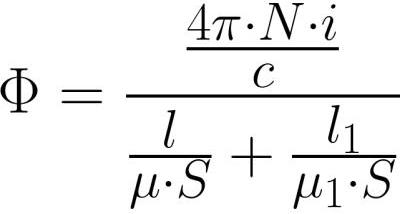
તે જોવાનું સરળ છે કે, ઇલેક્ટ્રિકલ સર્કિટ માટે ઓહ્મના કાયદામાં ઇએમએફની જેમ, એમ.ડી.એસ.

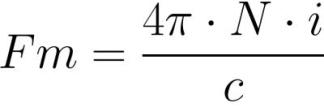
અહીં ઇલેક્ટ્રોમોટિવ બળ અને ચુંબકીય પ્રતિકારની ભૂમિકા ભજવે છે

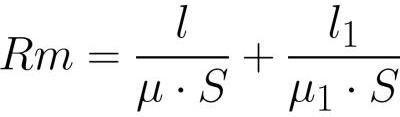
પ્રતિકારની ભૂમિકા (સાદ્રશ્ય દ્વારા ક્લાસિકલ ઓહ્મના કાયદા સાથે).