સપાટી અસર અને નિકટતા અસર

પ્રત્યક્ષ પ્રવાહ માટે વાહકનો પ્રતિકાર જાણીતા સૂત્ર ro =ρl / S દ્વારા નક્કી કરવામાં આવે છે.

આ પ્રતિકાર સતત વર્તમાન IO અને પાવર PO ની તીવ્રતા જાણીને પણ નક્કી કરી શકાય છે:

ro = PO / AzO2

તે તારણ આપે છે કે વૈકલ્પિક વર્તમાન સર્કિટમાં, સમાન વાહકનો પ્રતિકાર r પ્રતિકારક સ્થિર પ્રવાહ કરતા વધારે છે: r> rО

આ પ્રતિકાર r સીધા વર્તમાન પ્રતિકાર rO થી વિપરીત છે અને તેને સક્રિય પ્રતિકાર કહેવામાં આવે છે. વાયર પ્રતિકારમાં વધારો એ હકીકત દ્વારા સમજાવવામાં આવે છે કે વૈકલ્પિક પ્રવાહ સાથે, વર્તમાન ઘનતા વાયરના ક્રોસ વિભાગમાં જુદા જુદા બિંદુઓ પર સમાન હોતી નથી. મારી પાસે વાહક સપાટીઓ છે, વર્તમાન ઘનતા પ્રત્યક્ષ પ્રવાહ કરતા વધારે છે, અને કેન્દ્ર નાનું છે.

ઉચ્ચ આવર્તન પર, અનિયમિતતા એટલી ઝડપથી દેખાય છે કે કંડક્ટરના ક્રોસ સેક્શનની નોંધપાત્ર કેન્દ્રીય શુદ્ધતામાં વર્તમાન ઘનતા વ્યવહારીક રીતે શૂન્ય છે., વર્તમાન માત્ર સપાટીના સ્તરમાં પસાર થાય છે, તેથી જ આ ઘટનાને સપાટીની અસર કહેવામાં આવે છે.

આમ, સપાટીની અસર કંડક્ટરના ક્રોસ-સેક્શનમાં ઘટાડો તરફ દોરી જાય છે જેના દ્વારા વર્તમાન પ્રવાહ (સક્રિય ક્રોસ-સેક્શન) થાય છે, અને તેથી સીધા વર્તમાન પ્રતિકારની તુલનામાં તેના પ્રતિકારમાં વધારો થાય છે.

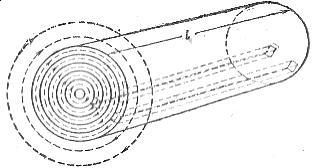
સપાટીની અસરનું કારણ સમજાવવા માટે, એક નળાકાર વાહક (ફિગ. 1) ની કલ્પના કરો, જેમાં સમાન ક્રોસ-સેક્શનના મોટી સંખ્યામાં પ્રાથમિક વાહક હોય, એકબીજાની નજીક હોય અને કેન્દ્રિત સ્તરોમાં ગોઠવાયેલા હોય.

ρl/S સૂત્ર દ્વારા મળેલ ડાયરેક્ટ કરંટ માટે આ વાયરનો પ્રતિકાર સમાન હશે.

ચોખા. 1. નળાકાર વાહકનું ચુંબકીય ક્ષેત્ર.

વૈકલ્પિક વિદ્યુત પ્રવાહ દરેક વાયરની આસપાસ વૈકલ્પિક ચુંબકીય ક્ષેત્ર બનાવે છે (ફિગ. 1). દેખીતી રીતે, અક્ષની નજીક સ્થિત પ્રાથમિક વાહક મોટા ચુંબકીય પ્રવાહ સપાટીના વાહકથી ઘેરાયેલો છે, તેથી પહેલાની સરખામણીમાં ઇન્ડક્ટન્સ અને પ્રેરક પ્રતિક્રિયા વધારે છે.

ધરી સાથે અને સપાટી પર સ્થિત લંબાઈના પ્રારંભિક વાયરના છેડા પર સમાન વોલ્ટેજ પર, પ્રથમમાં વર્તમાન ઘનતા બીજા કરતા ઓછી છે.

અક્ષ સાથે અને વાહકની પરિઘ સાથે વર્તમાન ઘનતા v વચ્ચેનો તફાવત વાહક d ના વ્યાસમાં વધારો, સામગ્રી γ ની વાહકતા, સામગ્રીની ચુંબકીય અભેદ્યતા μ અને AC આવર્તન સાથે વધે છે.

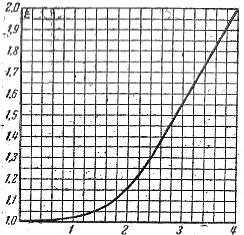
વાહક r ના સક્રિય પ્રતિકારનો ગુણોત્તર અને તેના પ્રતિકાર પર. ડાયરેક્ટ કરંટ rО ને ત્વચાની અસરનો ગુણાંક કહેવામાં આવે છે અને તે ξ (xi) અક્ષર દ્વારા સૂચવવામાં આવે છે, તેથી, ગુણાંક ξ અંજીરના ગ્રાફ પરથી નક્કી કરી શકાય છે. 2, જે ઉત્પાદન d અને √γμμое પર ξ ની અવલંબન દર્શાવે છે.

ચોખા. 2. ત્વચા અસર ગુણાંક નક્કી કરવા માટેનો ચાર્ટ.

આ ઉત્પાદનની ગણતરી કરતી વખતે, d ને cm, γ — 1 / ohm-cm માં, μo — v gn/ cm અને f = Hz માં દર્શાવવું જોઈએ.

એક ઉદાહરણ. ત્વચાની અસરના ગુણાંકને નિર્ધારિત કરવું જરૂરી છે કારણ કે હું f = 150 Hz ની આવર્તન પર d= 11.3 mm (S = 100 mm2) ના વ્યાસ સાથે કોપર વાહક છું.

સારુ કામ.

ફિગ માં ગ્રાફ અનુસાર. 2 આપણે ξ = 1.03 શોધીએ છીએ

વાહકમાં અસમાન વર્તમાન ઘનતા પડોશી વાહકોમાં પ્રવાહોના પ્રભાવને કારણે પણ થાય છે. આ ઘટનાને નિકટતા અસર કહેવામાં આવે છે.

બે સમાંતર વાહકમાં સમાન દિશામાં પ્રવાહોના ચુંબકીય ક્ષેત્રને ધ્યાનમાં લેતા, તે બતાવવાનું સરળ છે કે વિવિધ વાહક સાથે જોડાયેલા તે પ્રાથમિક વાહક, જે એકબીજાથી સૌથી દૂર છે, તે સૌથી નાના ચુંબકીય પ્રવાહ સાથે જોડાયેલા છે, તેથી તેમાં વર્તમાન ઘનતા સૌથી વધુ છે. જો સમાંતર વાયરમાં પ્રવાહોની દિશા જુદી જુદી હોય, તો તે બતાવી શકાય છે કે એકબીજાની સૌથી નજીકના વિવિધ વાયરો સાથે જોડાયેલા તે પ્રાથમિક વાયરોમાં ઉચ્ચ પ્રવાહની ઘનતા જોવા મળે છે.