ઇલેક્ટ્રિક ક્ષેત્રની લાક્ષણિકતાઓ

લેખ ઇલેક્ટ્રિક ક્ષેત્રની મુખ્ય લાક્ષણિકતાઓનું વર્ણન કરે છે: સંભવિત, વોલ્ટેજ અને તીવ્રતા.

ઇલેક્ટ્રિક ક્ષેત્ર શું છે

ઇલેક્ટ્રિક ક્ષેત્ર બનાવવા માટે, ઇલેક્ટ્રિક ચાર્જ બનાવવો જરૂરી છે. ચાર્જીસ (ચાર્જ્ડ બોડીઝ) ની આસપાસની જગ્યાના ગુણધર્મો તે જગ્યાના ગુણધર્મોથી અલગ છે જેમાં કોઈ ચાર્જ નથી. તે જ સમયે, અવકાશના ગુણધર્મો, જ્યારે તેમાં ઇલેક્ટ્રિક ચાર્જ દાખલ કરવામાં આવે છે, ત્યારે તે તરત જ બદલાતા નથી: પરિવર્તન ચાર્જથી શરૂ થાય છે અને અવકાશના એક બિંદુથી બીજા સ્થાને ચોક્કસ ગતિ સાથે ફેલાય છે.

ચાર્જ ધરાવતી અવકાશમાં, તે જગ્યામાં દાખલ કરાયેલા અન્ય ચાર્જ પર કાર્ય કરતી યાંત્રિક શક્તિઓ પ્રગટ થાય છે. આ દળો બીજા પર એક ચાર્જની સીધી ક્રિયાનું પરિણામ નથી, પરંતુ ગુણાત્મક રીતે બદલાયેલ માધ્યમ દ્વારા ક્રિયાનું પરિણામ છે.

ઈલેક્ટ્રિક ચાર્જની આસપાસની જગ્યા, જેમાં તેમાં દાખલ કરાયેલા ઈલેક્ટ્રિક ચાર્જ પર કાર્ય કરતા દળો પ્રગટ થાય છે, તેને ઇલેક્ટ્રિક ફિલ્ડ કહેવામાં આવે છે.

ઇલેક્ટ્રિક ફિલ્ડમાં ચાર્જ ક્ષેત્રની બાજુથી તેના પર કાર્ય કરતા બળની દિશામાં આગળ વધે છે.આવા ચાર્જની બાકીની સ્થિતિ ત્યારે જ શક્ય બને છે જ્યારે ઇલેક્ટ્રિક ફિલ્ડની મજબૂતાઈને સંતુલિત કરતા ચાર્જ પર અમુક બાહ્ય (બાહ્ય) બળ લાગુ કરવામાં આવે.

જલદી બાહ્ય બળ અને ક્ષેત્રીય શક્તિ વચ્ચેનું સંતુલન ખલેલ પહોંચે છે, ચાર્જ ફરીથી ખસેડવાનું શરૂ કરે છે. તેની હિલચાલની દિશા હંમેશા મોટા બળની દિશા સાથે એકરુપ હોય છે.

સ્પષ્ટતા માટે, ઇલેક્ટ્રિક ક્ષેત્ર સામાન્ય રીતે કહેવાતા ઇલેક્ટ્રિક ક્ષેત્ર રેખાઓ દ્વારા રજૂ થાય છે. આ રેખાઓ ઇલેક્ટ્રિક ફિલ્ડમાં કામ કરતા દળોની દિશા સાથે સુસંગત છે. તે જ સમયે, એટલી બધી રેખાઓ દોરવા માટે સંમતિ આપવામાં આવી હતી કે રેખાઓ પર કાટખૂણે સ્થાપિત વિસ્તારના દરેક 1 સેમી 2 માટે તેમની સંખ્યા અનુરૂપ બિંદુ પર ક્ષેત્રની મજબૂતાઈના પ્રમાણસર હતી.

ક્ષેત્રની દિશા સામાન્ય રીતે આપેલ ક્ષેત્રમાં મૂકવામાં આવેલા હકારાત્મક ચાર્જ પર કાર્ય કરતી ક્ષેત્રની શક્તિની દિશા તરીકે લેવામાં આવે છે. હકારાત્મક શુલ્ક હકારાત્મક શુલ્ક દ્વારા ભગાડવામાં આવે છે અને નકારાત્મક શુલ્ક તરફ આકર્ષાય છે. તેથી, ક્ષેત્રને હકારાત્મકથી નકારાત્મક શુલ્ક તરફ નિર્દેશિત કરવામાં આવે છે.

બળની રેખાઓની દિશા તીર દ્વારા રેખાંકનોમાં દર્શાવેલ છે. વિજ્ઞાને સાબિત કર્યું છે કે વિદ્યુત ક્ષેત્રના બળની રેખાઓની શરૂઆત અને અંત હોય છે, એટલે કે, તે પોતે બંધ થતી નથી. ક્ષેત્રની ધારવામાં આવેલી દિશાના આધારે, અમે શોધીએ છીએ કે બળની રેખાઓ હકારાત્મક ચાર્જ (પોઝિટિવલી ચાર્જ્ડ બોડી) સાથે શરૂ થાય છે અને નકારાત્મક સાથે સમાપ્ત થાય છે.

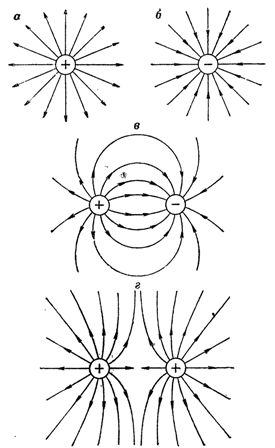
ચોખા. 1. બળની રેખાઓનો ઉપયોગ કરીને ઇલેક્ટ્રિક ક્ષેત્રની છબીના ઉદાહરણો: a — એક જ સકારાત્મક ચાર્જ સાથેનું ઇલેક્ટ્રિક ક્ષેત્ર, b — એક નકારાત્મક ચાર્જ સાથેનું ઇલેક્ટ્રિક ક્ષેત્ર, c — બે વિરોધી ચાર્જનું ઇલેક્ટ્રિક ક્ષેત્ર, d — એક બે જેવા ચાર્જનું વિદ્યુત ક્ષેત્ર

અંજીરમાં.1 બળની રેખાઓનો ઉપયોગ કરીને દર્શાવવામાં આવેલા ઇલેક્ટ્રિક ક્ષેત્રના ઉદાહરણો બતાવે છે. તે યાદ રાખવું આવશ્યક છે કે ઇલેક્ટ્રિક ફીલ્ડ લાઇન એ ક્ષેત્રને ગ્રાફિકલી રીતે રજૂ કરવાની માત્ર એક રીત છે. અહીં ફોર્સ કન્સેપ્ટની લાઇનનો કોઈ મોટો પદાર્થ નથી.

કુલોમ્બનો કાયદો

બે ચાર્જ વચ્ચેની ક્રિયાપ્રતિક્રિયાની શક્તિ ચાર્જના કદ અને પરસ્પર ગોઠવણી તેમજ તેમના પર્યાવરણના ભૌતિક ગુણધર્મો પર આધારિત છે.

બે ઇલેક્ટ્રિફાઇડ ભૌતિક સંસ્થાઓ માટે, જેનાં પરિમાણો શરીર વચ્ચેના અંતરની તુલનામાં નજીવા છે, ક્રિયાપ્રતિક્રિયાની સારવાર નીચે પ્રમાણે ગાણિતિક રીતે નક્કી કરવામાં આવે છે:

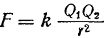
જ્યાં F એ ન્યૂટન (N) માં ચાર્જની ક્રિયાપ્રતિક્રિયાનું બળ છે, k — મીટર (m), Q1 અને Q2 માં ચાર્જ વચ્ચેનું અંતર — કુલમ્બ્સ (k) માં ઇલેક્ટ્રિક ચાર્જની તીવ્રતા, k એ પ્રમાણસરતા ગુણાંક છે, જેનું મૂલ્ય ચાર્જની આસપાસના માધ્યમના ગુણધર્મો પર આધાર રાખે છે.

ઉપરોક્ત સૂત્ર આ રીતે વાંચે છે: બે પોઈન્ટ ચાર્જ વચ્ચેની ક્રિયાપ્રતિક્રિયાનું બળ આ ચાર્જની તીવ્રતાના ઉત્પાદનના સીધા પ્રમાણસર છે અને તેમની વચ્ચેના અંતરના વર્ગના વિપરિત પ્રમાણસર છે (કુલોમ્બનો કાયદો).

પ્રમાણસરતા પરિબળ k નક્કી કરવા માટે, k = 1 /(4πεεO) અભિવ્યક્તિનો ઉપયોગ કરો.

ઇલેક્ટ્રિક ક્ષેત્ર સંભવિત

જો ચાર્જ પર કામ કરતા ક્ષેત્ર દળો કોઈપણ બાહ્ય દળો દ્વારા સંતુલિત ન હોય તો ઇલેક્ટ્રિક ક્ષેત્ર હંમેશા ચાર્જને ગતિ આપે છે. આ સૂચવે છે કે વિદ્યુત ક્ષેત્ર સંભવિત ઊર્જા ધરાવે છે, એટલે કે, કાર્ય કરવાની ક્ષમતા.

ચાર્જને અવકાશમાં એક બિંદુથી બીજા સ્થાને ખસેડવાથી, વિદ્યુત ક્ષેત્ર કાર્ય કરે છે, જેના પરિણામે ક્ષેત્રને સંભવિત ઊર્જાનો પુરવઠો ઘટે છે.જો કોઈ ચાર્જ ક્ષેત્ર દળોની વિરુદ્ધ કામ કરતા કેટલાક બાહ્ય બળની ક્રિયા હેઠળ ઇલેક્ટ્રિક ક્ષેત્રમાં ફરે છે, તો પછી કાર્ય ઇલેક્ટ્રિક ક્ષેત્ર દળો દ્વારા નહીં, પરંતુ બાહ્ય દળો દ્વારા કરવામાં આવે છે. આ કિસ્સામાં, ક્ષેત્રની સંભવિત ઊર્જા માત્ર ઘટતી નથી, પરંતુ, તેનાથી વિપરીત, વધે છે.

ઇલેક્ટ્રિક ફિલ્ડમાં ચાર્જને ખસેડતા બાહ્ય બળ દ્વારા કરવામાં આવેલું કાર્ય તે ગતિનો વિરોધ કરતા ક્ષેત્ર દળોની તીવ્રતાના પ્રમાણસર છે. બાહ્ય દળો દ્વારા આ કિસ્સામાં કરવામાં આવેલ કાર્ય સંપૂર્ણપણે ક્ષેત્રની સંભવિત ઊર્જાને વધારવા માટે ખર્ચવામાં આવે છે. ક્ષેત્રને તેની સંભવિત ઉર્જાની બાજુથી દર્શાવવા માટે, ઇલેક્ટ્રિક ફિલ્ડ પોટેન્શિયલ નામના જથ્થાને કહેવામાં આવે છે.

આ જથ્થાનો સાર નીચે મુજબ છે. ધારો કે હકારાત્મક ચાર્જ વિચારણા હેઠળના ઇલેક્ટ્રિક ક્ષેત્રની બહાર છે. આનો અર્થ એ છે કે આપેલ ચાર્જ પર ક્ષેત્રની વ્યવહારીક રીતે કોઈ અસર થતી નથી. બાહ્ય બળ આ ચાર્જને ઇલેક્ટ્રિક ફિલ્ડમાં દાખલ કરવા દો અને, ક્ષેત્ર દળો દ્વારા કરવામાં આવતી ગતિના પ્રતિકારને દૂર કરીને, ચાર્જને ક્ષેત્રમાં આપેલ બિંદુ પર ખસેડો. બળ દ્વારા કરવામાં આવેલ કાર્ય, અને તેથી જથ્થા કે જેના દ્વારા ક્ષેત્રની સંભવિત ઊર્જામાં વધારો થયો છે, તે ક્ષેત્રના ગુણધર્મો પર સંપૂર્ણપણે આધાર રાખે છે. તેથી, આ કાર્ય આપેલ વિદ્યુત ક્ષેત્રની ઊર્જાને લાક્ષણિકતા આપી શકે છે.

ફિલ્ડમાં આપેલ બિંદુ પર મૂકવામાં આવેલા ધન ચાર્જના એકમ સાથે સંબંધિત ઇલેક્ટ્રિક ક્ષેત્ર ઊર્જાને આપેલ બિંદુ પર ક્ષેત્ર સંભવિત કહેવામાં આવે છે.

જો પોટેન્શિયલ φ અક્ષર દ્વારા દર્શાવવામાં આવે છે, q અક્ષર દ્વારા ચાર્જ અને W દ્વારા ચાર્જ ખસેડવા માટે ખર્ચવામાં આવેલ કાર્ય, તો આપેલ બિંદુ પર ક્ષેત્ર સંભવિત સૂત્ર φ = W/q દ્વારા દર્શાવવામાં આવશે.

તે અનુસરે છે કે આપેલ બિંદુ પર વિદ્યુત ક્ષેત્રની સંભવિતતા આંકડાકીય રીતે બાહ્ય બળ દ્વારા કરવામાં આવેલ કાર્યની બરાબર છે જ્યારે એકમ હકારાત્મક ચાર્જ ક્ષેત્રની બહાર આપેલ બિંદુ તરફ જાય છે. ક્ષેત્ર સંભવિત વોલ્ટ (V) માં માપવામાં આવે છે. જો ક્ષેત્રની બહાર આપેલ બિંદુ પર એક કુલંબ વીજળીના સ્થાનાંતરણ દરમિયાન, બાહ્ય દળોએ એક જૌલ જેટલું કામ કર્યું હોય, તો ક્ષેત્રમાં આપેલ બિંદુ પર સંભવિત એક વોલ્ટ બરાબર છે: 1 વોલ્ટ = 1 જૌલ / 1 કુલોમ્બ

ઇલેક્ટ્રિક ક્ષેત્રની તાકાત

કોઈપણ વિદ્યુત ક્ષેત્રમાં, હકારાત્મક ચાર્જ ઉચ્ચ સંભવિતતાના બિંદુઓથી નીચી સંભવિતતાના બિંદુઓ તરફ જાય છે. તેનાથી વિપરીત, નકારાત્મક શુલ્ક નીચી સંભવિતતાના બિંદુઓથી ઉચ્ચ સંભવિતતાના બિંદુઓ તરફ જાય છે. બંને કિસ્સાઓમાં, કામ ઇલેક્ટ્રિક ક્ષેત્રની સંભવિત ઊર્જાના ખર્ચે કરવામાં આવે છે.

જો આપણે આ કાર્યને જાણીએ, એટલે કે, જ્યારે હકારાત્મક ચાર્જ q ક્ષેત્રના બિંદુ 1 થી બિંદુ 2 તરફ જાય ત્યારે ક્ષેત્રની સંભવિત ઊર્જામાં ઘટાડો થયો છે, તો પછી આ બિંદુઓ વચ્ચેનો વોલ્ટેજ શોધવાનું સરળ છે. ક્ષેત્ર U1,2:

U1,2 = A/q,

જ્યાં A એ ક્ષેત્ર દળો દ્વારા કરવામાં આવેલું કાર્ય છે જ્યારે ચાર્જ q બિંદુ 1 થી બિંદુ 2 માં સ્થાનાંતરિત થાય છે. વિદ્યુત ક્ષેત્રના બે બિંદુઓ વચ્ચેનો વોલ્ટેજ સંખ્યાત્મક રીતે શૂન્ય દ્વારા એક બિંદુથી એકમ હકારાત્મક ચાર્જને સ્થાનાંતરિત કરવા માટે કરવામાં આવતા કાર્યની બરાબર છે. બીજા ક્ષેત્રમાં.

જેમ જોઈ શકાય છે, ક્ષેત્રના બે બિંદુઓ વચ્ચેનો વોલ્ટેજ અને સમાન બિંદુઓ વચ્ચેનો સંભવિત તફાવત એ જ ભૌતિક એકમનું પ્રતિનિધિત્વ કરે છે... તેથી, શરતો વોલ્ટેજ અને સંભવિત તફાવત સમાન છે. વોલ્ટેજ વોલ્ટ (V) માં માપવામાં આવે છે.

બે બિંદુઓ વચ્ચેનો વોલ્ટેજ એક વોલ્ટ જેટલો છે જો, જ્યારે એક કૂલમ્બ વીજળીને ક્ષેત્રના એક બિંદુથી બીજા સ્થાને સ્થાનાંતરિત કરવામાં આવે, ત્યારે ક્ષેત્ર દળો એક જૌલની બરાબર કાર્ય કરે છે: 1 વોલ્ટ = 1 જૌલ / 1 કૂલમ્બ

ઇલેક્ટ્રિક ક્ષેત્રની તાકાત

કુલોમ્બના કાયદા પરથી તે અનુસરે છે કે આ ક્ષેત્રમાં મૂકવામાં આવેલા અન્ય ચાર્જ પર કાર્ય કરતા આપેલ ચાર્જની ઇલેક્ટ્રિક ક્ષેત્રની શક્તિ ક્ષેત્રના તમામ બિંદુઓ પર સમાન નથી. કોઈપણ બિંદુએ વિદ્યુત ક્ષેત્રને બળની તીવ્રતા દ્વારા વર્ગીકૃત કરી શકાય છે જેની સાથે તે આપેલ બિંદુ પર મૂકવામાં આવેલા એકમ હકારાત્મક ચાર્જ પર કાર્ય કરે છે.

આ મૂલ્યને જાણીને, દરેક ચાર્જ Q પર કાર્ય કરતું બળ F નક્કી કરી શકાય છે. તમે લખી શકો છો કે F = Q x E, જ્યાં F એ ઇલેક્ટ્રિક ક્ષેત્ર દ્વારા ક્ષેત્રમાં એક બિંદુ પર મૂકવામાં આવેલા Q ચાર્જ પર કાર્ય કરતું બળ છે, E છે ક્ષેત્રમાં સમાન બિંદુ પર મૂકવામાં આવેલ એકમ હકારાત્મક ચાર્જ પર કાર્ય કરતું બળ. ક્ષેત્રના આપેલ બિંદુ પર એકમ હકારાત્મક ચાર્જ દ્વારા અનુભવાતા બળની સંખ્યાત્મક રીતે E સંખ્યાને ઇલેક્ટ્રિક ક્ષેત્રની તાકાત કહેવામાં આવે છે.