સિંગલ ફેઝ વૈકલ્પિક પ્રવાહ

વૈકલ્પિક પ્રવાહ પ્રાપ્ત કરવો

જો વાયર A ઘડિયાળની દિશામાં ચુંબકના બે ધ્રુવો દ્વારા રચાયેલા ચુંબકીય પ્રવાહમાં ફેરવવામાં આવે છે (ફિગ. 1), તો જ્યારે વાયર ચુંબકીય ક્ષેત્રની રેખાઓને પાર કરે છે, ત્યારે તે ઇ. ડી. s જેની કિંમત અભિવ્યક્તિ દ્વારા નક્કી કરવામાં આવે છે

E = Blvsinα,

જ્યાં B એ T માં ચુંબકીય ઇન્ડક્શન છે, l એ m માં વાયરની લંબાઈ છે, v એ m/s માં વાયરની ગતિ છે, α — એ કોણ કે જેના પર વાયર ચુંબકીય ક્ષેત્રની રેખાઓને પાર કરે છે.

આ કેસ માટે B, I અને v સ્થિર રહેવા દો, પછી પ્રેરિત e. વગેરે c. માત્ર કોણ α પર આધાર રાખે છે કે જેના પર વાયર ચુંબકીય ક્ષેત્રને પાર કરે છે. તેથી, બિંદુ 1 પર, જ્યારે વાયર ચુંબકીય ક્ષેત્ર રેખાઓ સાથે આગળ વધે છે, ત્યારે પ્રેરિત emf નું મૂલ્ય. વગેરે જ્યારે વાયર પોઈન્ટ 3 oe તરફ જશે ત્યારે p શૂન્ય હશે. વગેરે v. સૌથી વધુ મહત્વ ધરાવશે, કારણ કે બળની રેખાઓ વાહક દ્વારા તેમને લંબરૂપ દિશામાં ઓળંગવામાં આવશે, અને અંતે, દા.ત. વગેરે જો વાયરને પોઈન્ટ 5 પર ખસેડવામાં આવે તો v. ફરીથી શૂન્ય પર પહોંચી જશે.

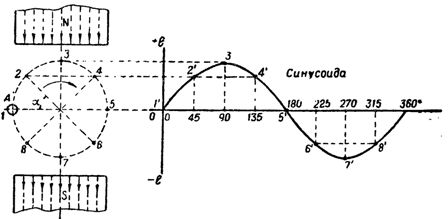
ચોખા. 1. પ્રેરિત ઇ બદલવાનું. વગેરે ચુંબકીય ક્ષેત્રમાં ફરતા વાયરમાં pp

મધ્યવર્તી બિંદુઓ 2 અને 4 પર, જેમાં વાયર α = 45 °, પ્રેરિત emf ની કિંમત પર બળની રેખાઓને પાર કરે છે. વગેરે c. બિંદુ 3 કરતાં અનુરૂપ રીતે ઓછું હશે. આમ, જ્યારે વાયર બિંદુ 1 થી બિંદુ 5 તરફ વળે છે, એટલે કે, 180 ° દ્વારા, પ્રેરિત e. વગેરે v. શૂન્યથી મહત્તમ અને પાછા શૂન્યમાં બદલાય છે.

તે તદ્દન સ્પષ્ટ છે કે વાયર A ના વધુ પરિભ્રમણ પર 180 ° (બિંદુ 6, 7, 8 અને 1 દ્વારા) ના ખૂણા દ્વારા, પ્રેરિત e માં ફેરફારની પ્રકૃતિ. વગેરે p. સમાન હશે, પરંતુ તેની દિશા વિરુદ્ધમાં બદલાશે, કારણ કે વાયર અન્ય ધ્રુવની નીચે પહેલેથી જ ચુંબકીય ક્ષેત્રની રેખાઓને પાર કરશે, જે તેમને વિરુદ્ધ પ્રથમ દિશામાં ક્રોસ કરવા સમાન છે.

તેથી, જ્યારે વાયરને 360 ° ફેરવવામાં આવે છે, ત્યારે પ્રેરિત ઇ. વગેરે v. માત્ર તીવ્રતામાં દરેક સમયે ફેરફાર થતો નથી, પરંતુ તેની દિશા પણ બે વાર બદલાય છે.

જો વાયર અમુક પ્રતિકાર માટે બંધ હોય તો વાયર દેખાશે વીજળી, કદ અને દિશામાં પણ બદલાય છે.

વિદ્યુત પ્રવાહ, તીવ્રતા અને દિશામાં સતત બદલાતા રહે છે, તેને વૈકલ્પિક પ્રવાહ કહેવામાં આવે છે.

સાઈન વેવ શું છે?

ફેરફારની પ્રકૃતિ ઇ. વગેરે (વર્તમાન) વધુ સ્પષ્ટતા માટે વાયરના એક વળાંક માટે, તેઓ ગ્રાફિકલી વળાંકનો ઉપયોગ કરીને રજૂ થાય છે. ઇ ની કિંમત હોવાથી. વગેરે c. sinα ના પ્રમાણસર, પછી, ચોક્કસ ખૂણા સેટ કર્યા પછી, કોષ્ટકોની મદદથી, દરેક ખૂણાના સાઈનનું મૂલ્ય નક્કી કરવું અને e ના ફેરફાર માટે વળાંક બાંધવા માટે યોગ્ય સ્કેલ પર શક્ય છે. વગેરે c. આ કરવા માટે, આડી ધરી પર આપણે વાયરના પરિભ્રમણના ખૂણાઓને બાજુએ રાખીશું, અને ઊભી ધરી પર, યોગ્ય સ્કેલમાં, પ્રેરિત e. વગેરે સાથે

જો અગાઉ ફિગમાં દર્શાવેલ છે.1 બિંદુઓને સરળ વક્ર રેખા સાથે જોડો, પછી તે પ્રેરિત e માં પરિવર્તનની તીવ્રતા અને પ્રકૃતિનો ખ્યાલ આપશે. વગેરે (વર્તમાન) ચુંબકીય ક્ષેત્રમાં વાહકની કોઈપણ સ્થિતિ પર. એ હકીકતને કારણે કે પ્રેરિત ઇ.ની કિંમત. વગેરે p. કોઈપણ ક્ષણે એ કોણની સાઈન દ્વારા નક્કી કરવામાં આવે છે કે જેના પર વાયર અંજીરમાં બતાવેલ ચુંબકીય ક્ષેત્રને પાર કરે છે. 1 વળાંકને સાઇનસૉઇડ કહેવામાં આવે છે, અને ઇ. વગેરે s. — સાઇનસૉઇડલ.

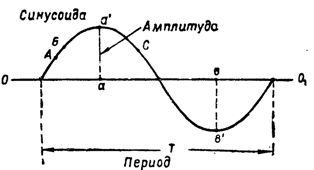
ચોખા. 2. સાઇનસૉઇડ અને તેના લાક્ષણિક મૂલ્યો

અમે જે ફેરફારો જોયા તે e. વગેરે c. 360 °ના ખૂણા પર ચુંબકીય ક્ષેત્રમાં વાયરના પરિભ્રમણને સાઇનસોઇડ રીતે અનુરૂપ છે. જ્યારે વાયરને આગામી 360 ° પર ફેરવવામાં આવે છે, ત્યારે પ્રેરિત e માં ફેરફારો થાય છે. વગેરે s.(અને વર્તમાન) ફરીથી સાઈન વેવમાં દેખાશે, એટલે કે, તેઓ સમયાંતરે પુનરાવર્તિત થશે.

તદનુસાર, આ કારણે ઇ. વગેરે c. ને વિદ્યુત પ્રવાહ sinusoidal alternating current કહેવામાં આવે છે... તે એકદમ સ્પષ્ટ છે કે બંધ બાહ્ય સર્કિટની હાજરીમાં, વાયર A ના છેડે આપણા દ્વારા માપી શકાય તેવો વોલ્ટેજ પણ sinusoidal રીતે બદલાશે.

ચુંબકીય પ્રવાહ અથવા કોઇલમાં જોડાયેલા વાયરની સિસ્ટમમાં વાયરને ફેરવીને મેળવવામાં આવતા વૈકલ્પિક પ્રવાહને સિંગલ-ફેઝ વૈકલ્પિક પ્રવાહ કહેવામાં આવે છે.

સિનુસોઇડલ વૈકલ્પિક પ્રવાહો ટેકનોલોજીમાં સૌથી વધુ ઉપયોગમાં લેવાય છે. જો કે, તમે વૈકલ્પિક પ્રવાહો શોધી શકો છો જે સાઈન કાયદા અનુસાર બદલાતા નથી. આવા વૈકલ્પિક પ્રવાહોને નોન-સાઇનસોઇડલ કહેવામાં આવે છે.

આ પણ જુઓ: વૈકલ્પિક પ્રવાહ શું છે અને તે સીધા પ્રવાહથી કેવી રીતે અલગ છે

કંપનવિસ્તાર, અવધિ, સિંગલ-ફેઝ વૈકલ્પિક પ્રવાહની આવર્તન

વર્તમાન તાકાત, સાઇનસૉઇડ સાથે બદલાતા, સતત બદલાતા રહે છે. તેથી, જો બિંદુ A (ફિગ. 2) પર વર્તમાન 3a ની બરાબર છે, તો બિંદુ B પર તે પહેલેથી જ વધારે હશે.સાઇનસૉઇડ પરના અન્ય કોઈ બિંદુએ, ઉદાહરણ તરીકે બિંદુ C પર, વર્તમાનમાં હવે નવું મૂલ્ય હશે, વગેરે.

ચોક્કસ સમયે જ્યારે તે સાઇનસૉઇડ સાથે બદલાય છે ત્યારે વર્તમાનની મજબૂતાઈને તાત્કાલિક વર્તમાન મૂલ્યો કહેવામાં આવે છે.

સિંગલ-ફેઝ વૈકલ્પિક પ્રવાહનું સૌથી મોટું ત્વરિત મૂલ્ય કહેવામાં આવે છે જ્યારે તે સાઇનસૉઇડલ કંપનવિસ્તાર સાથે બદલાય છે... તે જોવાનું સરળ છે કે વાયરના એક વળાંક માટે પ્રવાહ તેના કંપનવિસ્તાર મૂલ્ય સુધી બે વાર પહોંચે છે. aa' નું એક મૂલ્ય સકારાત્મક છે અને તે 001 અક્ષ પરથી દોરવામાં આવ્યું છે અને બીજું bv 'નકારાત્મક છે અને ધરીથી નીચે દોરવામાં આવ્યું છે.

જે સમય દરમિયાન પ્રેરિત ઇ. વગેરે (અથવા વર્તમાન બળ) ફેરફારોના સમગ્ર ચક્રમાંથી પસાર થાય છે, કહેવાતા માસિક ચક્ર T (ફિગ. 2). સમયગાળો સામાન્ય રીતે સેકંડમાં માપવામાં આવે છે.

સમયગાળાના પારસ્પરિકને આવર્તન (f) કહેવામાં આવે છે. બીજા શબ્દો માં, વૈકલ્પિક વર્તમાન આવર્તન એકમ સમય દીઠ સમયગાળાની સંખ્યા છે, એટલે કે. સેકન્ડમાં. તેથી, ઉદાહરણ તરીકે, જો 1 સેકન્ડની અંદર વૈકલ્પિક પ્રવાહ દસ વખત સમાન મૂલ્યો અને દિશા ધારે છે, તો આવા વૈકલ્પિક પ્રવાહની આવર્તન પ્રતિ સેકન્ડ 10 અવધિ હશે.

આવર્તન માપવા માટે, પ્રતિ સેકન્ડના સમયગાળાની સંખ્યાને બદલે, હર્ટ્ઝ (હર્ટ્ઝ) નામના એકમનો ઉપયોગ કરવામાં આવે છે. 1 હર્ટ્ઝની આવર્તન 1 એલપીએસ / સેકન્ડની આવર્તન બરાબર છે. ઉચ્ચ ફ્રીક્વન્સીઝને માપતી વખતે, હર્ટ્ઝ કરતા 1000 ગણા મોટા એકમનો ઉપયોગ કરવો વધુ અનુકૂળ છે, એટલે કે. કિલોહર્ટ્ઝ (kHz), અથવા હર્ટ્ઝ કરતાં 1,000,000 ગણો વધારે — મેગાહર્ટ્ઝ (mhz).

ટેક્નોલોજીમાં વપરાતા વૈકલ્પિક પ્રવાહોને, આવર્તનના આધારે, ઓછા-આવર્તન પ્રવાહો અને ઉચ્ચ-આવર્તન પ્રવાહોમાં વિભાજિત કરી શકાય છે.

AC rms મૂલ્ય

વાયરમાંથી પસાર થતો સીધો પ્રવાહ તેને ગરમ કરે છે. જો તમે વાયર દ્વારા વૈકલ્પિક પ્રવાહ ચલાવો છો, તો વાયર પણ ગરમ થશે.આ સમજી શકાય તેવું છે, કારણ કે વૈકલ્પિક પ્રવાહ હંમેશા તેની દિશા બદલતો હોવા છતાં, ગરમીનું પ્રકાશન વાયરમાં વર્તમાનની દિશા પર બિલકુલ આધાર રાખતું નથી.

જ્યારે વૈકલ્પિક પ્રવાહ લાઇટ બલ્બમાંથી પસાર થાય છે, ત્યારે તેનું ફિલામેન્ટ ચમકશે. 50 હર્ટ્ઝની પ્રમાણભૂત વૈકલ્પિક વર્તમાન આવર્તન પર, પ્રકાશની કોઈ ફ્લિકરિંગ થશે નહીં, કારણ કે અગ્નિથી પ્રકાશિત બલ્બના ફિલામેન્ટ, થર્મલ જડતા ધરાવે છે, તે સમયે જ્યારે સર્કિટમાં વર્તમાન શૂન્ય હોય છે ત્યારે તેને ઠંડુ થવાનો સમય નથી. લાઇટિંગ માટે 50 Hz કરતાં ઓછી આવર્તન સાથે વૈકલ્પિક પ્રવાહનો ઉપયોગ એ હકીકતને કારણે અનિચ્છનીય છે કે બલ્બની તીવ્રતામાં અપ્રિય, આંખને થકવી નાખે તેવી વધઘટ દેખાય છે.

પ્રત્યક્ષ વર્તમાન સામ્યતા ચાલુ રાખીને, અમે અપેક્ષા રાખી શકીએ છીએ કે વાયરમાંથી વહેતો વૈકલ્પિક પ્રવાહ તેની આસપાસ બનાવે છે. ચુંબકીય ક્ષેત્ર. વાસ્તવમાં n વૈકલ્પિક પ્રવાહ ચુંબકીય ક્ષેત્ર બનાવતું નથી, પરંતુ કારણ કે તે બનાવેલ ચુંબકીય ક્ષેત્ર પણ દિશા અને તીવ્રતામાં ચલ હશે.

વૈકલ્પિક પ્રવાહ દરેક સમયે તીવ્રતા અને દિશા એનએસ બંનેમાં બદલાય છે. સ્વાભાવિક રીતે, પ્રશ્ન ઊભો થાય છે કે ચલ T ને સારી રીતે કેવી રીતે માપવું, અને સાઇનસૉઇડ સાથે બદલાતી વખતે તેનું મૂલ્ય શું છે તે આ અથવા તે ક્રિયાને કારણભૂત ગણવું જોઈએ.

C આ હેતુ માટે, વૈકલ્પિક પ્રવાહની સરખામણી તે પ્રત્યક્ષ પ્રવાહ સાથે ઉત્પન્ન થતી ક્રિયાના સંદર્ભમાં કરવામાં આવે છે, જેનું મૂલ્ય પ્રયોગ દરમિયાન યથાવત રહે છે.

ધારો કે સતત પ્રતિકાર 10 A ના વાયરમાંથી સીધો પ્રવાહ વહે છે અને તે જાણવા મળે છે કે વાયર 50 ° તાપમાને ગરમ થાય છે.જો હવે આપણે સમાન વાયરમાંથી સીધો પ્રવાહ નહીં, પરંતુ વૈકલ્પિક પ્રવાહ પસાર કરીએ છીએ, અને તેથી આપણે તેનું મૂલ્ય પસંદ કરીએ છીએ (ઉદાહરણ તરીકે, રિઓસ્ટેટ સાથે) જેથી વાયર પણ 50 ° તાપમાને ગરમ થાય, તો પછી આ કિસ્સામાં આપણે કહી શકીએ કે વૈકલ્પિક પ્રવાહની ક્રિયા સીધી પ્રવાહની ક્રિયા જેટલી છે.

બંને સ્થિતિમાં વાયરને સમાન તાપમાને ગરમ કરવું એ દર્શાવે છે કે સમયના એકમમાં વૈકલ્પિક પ્રવાહ વાયરમાં સીધી પ્રવાહ જેટલી જ ગરમી આપે છે.

એક વૈકલ્પિક સિનુસોઇડલ પ્રવાહ કે જે એકમ સમય દીઠ આપેલ પ્રતિકાર માટે પ્રત્યક્ષ પ્રવાહની તીવ્રતામાં પ્રત્યક્ષ પ્રવાહની સમકક્ષ ગરમીની સમાન માત્રામાં ઉત્સર્જન કરે છે... આ વર્તમાન મૂલ્યને વૈકલ્પિક પ્રવાહનું અસરકારક (Id) અથવા અસરકારક મૂલ્ય કહેવામાં આવે છે.. તેથી, અમારા ઉદાહરણ માટે, વૈકલ્પિક પ્રવાહનું અસરકારક મૂલ્ય 10 A હશે... આ કિસ્સામાં, મહત્તમ (શિખર) વર્તમાન મૂલ્યો તીવ્રતામાં સરેરાશ મૂલ્યો કરતાં વધી જશે.

અનુભવ અને ગણતરીઓ દર્શાવે છે કે વૈકલ્પિક પ્રવાહના અસરકારક મૂલ્યો √2 (1.41) વખતમાં તેના કંપનવિસ્તારના મૂલ્યો કરતાં નાના છે. તેથી, જો વર્તમાનનું ટોચનું મૂલ્ય જાણીતું હોય, તો વર્તમાન Ia ના કંપનવિસ્તારને √2, એટલે કે Id = Aza/√2 વડે વિભાજીત કરીને વર્તમાન Id નું અસરકારક મૂલ્ય નક્કી કરી શકાય છે.

તેનાથી વિપરિત, જો વર્તમાનનું rms મૂલ્ય જાણીતું હોય, તો વર્તમાનની ટોચની કિંમતની ગણતરી કરી શકાય છે, એટલે કે Ia = Azd√2

e ના કંપનવિસ્તાર અને rms મૂલ્યો માટે સમાન સંબંધો રહેશે. વગેરે v. અને વોલ્ટેજ: એકમ = Ea /√2, Ud = Uа/√2

માપન ઉપકરણો મોટાભાગે વાસ્તવિક મૂલ્યો દર્શાવે છે, તેથી, જ્યારે સંકેત, અનુક્રમણિકા «d» સામાન્ય રીતે અવગણવામાં આવે છે, પરંતુ તમારે તેના વિશે ભૂલવું જોઈએ નહીં.

એસી સર્કિટ્સમાં અવરોધ

જ્યારે ઇન્ડક્ટન્સ અને કેપેસીટન્સ ઉપભોક્તાઓ એસી સર્કિટ સાથે જોડાયેલા હોય, ત્યારે સક્રિય અને પ્રતિક્રિયા બંનેને ધ્યાનમાં લેવું આવશ્યક છે (પ્રતિક્રિયા ત્યારે થાય છે જ્યારે કેપેસિટર ચાલુ હોય અથવા AC સર્કિટમાં ચોકક્સ). તેથી, આવા ઉપભોક્તામાંથી પસાર થતા વર્તમાનને નિર્ધારિત કરતી વખતે, સર્કિટ (ગ્રાહક) ના અવરોધ દ્વારા સપ્લાય વોલ્ટેજને વિભાજિત કરવું જરૂરી છે.

સિંગલ-ફેઝ એસી સર્કિટનું અવબાધ (Z) નીચેના સૂત્ર દ્વારા નક્કી કરવામાં આવે છે:

Z = √(R2 + (ωL — 1 / ωC)2

જ્યાં R એ ઓહ્મમાં સર્કિટનો સક્રિય પ્રતિકાર છે, L એ હેનરીમાં સર્કિટનો ઇન્ડક્ટન્સ છે, C એ ફરાડ્સમાં સર્કિટ (કેપેસિટર) ની કેપેસિટન્સ છે, ω — વૈકલ્પિક પ્રવાહની કોણીય આવર્તન.

વૈકલ્પિક વર્તમાન સર્કિટમાં વિવિધ ઉપભોક્તાઓનો ઉપયોગ કરવામાં આવે છે જ્યાં આર, એલ, સીના ત્રણ મૂલ્યો અથવા તેમાંના કેટલાકને ધ્યાનમાં લેવું જરૂરી છે. તે જ સમયે, વૈકલ્પિક પ્રવાહની કોણીય આવર્તન ધ્યાનમાં લેવી આવશ્યક છે.

કેટલાક વપરાશકર્તાઓ માટે, અનુરૂપ ખૂણાના આવર્તન મૂલ્યો પર ફક્ત R અને L ના મૂલ્યો ધ્યાનમાં લઈ શકાય છે. ઉદાહરણ તરીકે, 50 Hz ની AC આવર્તન પર સોલેનોઇડ કોઇલ અથવા જનરેટર વિન્ડિંગને માત્ર સક્રિય અને પ્રેરક પ્રતિકાર ધરાવતું ગણી શકાય. બીજા શબ્દોમાં કહીએ તો, આ કિસ્સામાં ક્ષમતાને અવગણી શકાય છે. પછી આવા વપરાશકર્તાના AC અવબાધની ગણતરી સૂત્ર દ્વારા કરી શકાય છે:

Z = √(R2 + ω2L2)

જો આવી કોઇલ અથવા કોઇલ વૈકલ્પિક વર્તમાન કામગીરી માટે રચાયેલ હોય તો તે સમાન વોલ્ટેજના સીધા પ્રવાહ સાથે જોડાયેલ હોય, તો કોઇલમાંથી ખૂબ જ મોટો પ્રવાહ વહેશે, જે નોંધપાત્ર ગરમી પેદા કરી શકે છે, અને કોઇલના ઇન્સ્યુલેશનને નુકસાન થઈ શકે છે. તેનાથી વિપરિત, ડાયરેક્ટ કરંટ સર્કિટમાં કામ કરવા માટે રચાયેલ કોઇલમાંથી એક નાનો પ્રવાહ વહે છે અને તે જ વોલ્ટેજના વૈકલ્પિક વર્તમાન સર્કિટ સાથે જોડાયેલ છે, અને જે ઉપકરણમાં આ કોઇલનો ઉપયોગ કરવામાં આવે છે તે જરૂરી ક્રિયા કરશે નહીં.

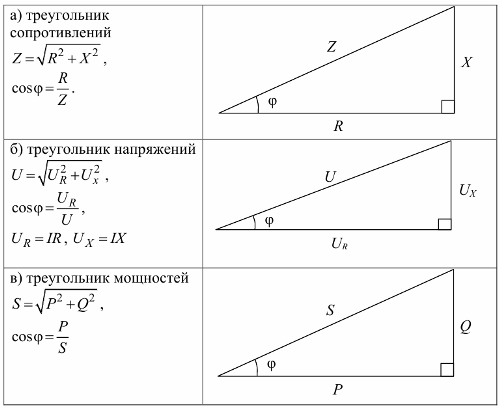
પ્રતિકાર ત્રિકોણ, વોલ્ટેજ ત્રિકોણ અને શક્તિ ત્રિકોણ: