ઇન્ડક્ટન્સની ગણતરી કેવી રીતે કરવી

જેમ મિકેનિક્સમાં સમૂહ ધરાવતું શરીર અવકાશમાં પ્રવેગકતાનો પ્રતિકાર કરે છે, જડતા પ્રગટ કરે છે, તેવી જ રીતે ઇન્ડક્ટન્સ કંડક્ટરમાં વર્તમાનને બદલાતા, સ્વ-ઇન્ડક્શન EMFને પ્રગટ કરતા અટકાવે છે. આ સ્વ-ઇન્ડક્શનનું EMF છે, જે વર્તમાનમાં ઘટાડો, તેને જાળવી રાખવાનો પ્રયાસ કરીને, અને વર્તમાનમાં વધારો, તેને ઘટાડવાનો પ્રયાસ કરીને બંનેનો વિરોધ કરે છે.

હકીકત એ છે કે સર્કિટમાં વર્તમાનને બદલવાની (વધતા અથવા ઘટાડાની) પ્રક્રિયામાં, આ વર્તમાન દ્વારા બનાવેલ ચુંબકીય પ્રવાહ પણ બદલાય છે, જે મુખ્યત્વે આ સર્કિટ દ્વારા મર્યાદિત વિસ્તારમાં સ્થાનિક છે. અને જેમ જેમ ચુંબકીય પ્રવાહ વધે છે અથવા ઘટે છે, તેમ તે સ્વ-ઇન્ડક્શનના EMFને પ્રેરિત કરે છે (લેન્ઝના નિયમ મુજબ - જે કારણથી તે થાય છે તેની વિરુદ્ધ, એટલે કે, શરૂઆતમાં ઉલ્લેખિત વર્તમાનની વિરુદ્ધ), બધું સમાન સર્કિટમાં. અહીં ઇન્ડક્ટન્સ L ને વર્તમાન I અને કુલ ચુંબકીય પ્રવાહ Φ વચ્ચેના પ્રમાણસરતા પરિબળ કહેવામાં આવે છે, આ વર્તમાન દ્વારા ઉત્પન્ન થાય છે:

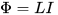
તેથી, સર્કિટનું ઇન્ડક્ટન્સ જેટલું ઊંચું છે, તે પરિણામી ચુંબકીય ક્ષેત્ર કરતાં વધુ મજબૂત છે, તે વર્તમાનને બદલાતા અટકાવે છે (તે ક્ષેત્ર જે તેને બનાવે છે) અને તેથી વધુ ઇન્ડક્ટન્સ દ્વારા વર્તમાનને બદલવામાં વધુ સમય લાગશે, સમાન લાગુ વોલ્ટેજ સાથે. નીચેનું વિધાન પણ સાચું છે: ઇન્ડક્ટન્સ જેટલું ઊંચું હશે, જ્યારે તેમાંથી ચુંબકીય પ્રવાહ બદલાશે ત્યારે સમગ્ર સર્કિટમાં વોલ્ટેજ વધુ હશે.

ધારો કે આપણે ચોક્કસ પ્રદેશમાં ચુંબકીય પ્રવાહને સ્થિર દરે બદલીએ છીએ, તો પછી આ પ્રદેશને વિવિધ સર્કિટ વડે આવરી લેવાથી, આપણને તે સર્કિટ પર વધુ વોલ્ટેજ મળશે જેની ઇન્ડક્ટન્સ વધારે છે (ટ્રાન્સફોર્મર, રુમકોર્ફ કોઇલ, વગેરે આ સિદ્ધાંત પર કામ કરે છે).

પરંતુ લૂપ ઇન્ડક્ટન્સની ગણતરી કેવી રીતે થાય છે? વર્તમાન અને ચુંબકીય પ્રવાહ વચ્ચે પ્રમાણસરતા પરિબળ કેવી રીતે શોધવું? યાદ રાખવાની પ્રથમ વસ્તુ એ છે કે હેનરી (એચ) માં ઇન્ડક્ટન્સ બદલાય છે. 1 હેનરીના ઇન્ડક્ટન્સ સાથેના સર્કિટના ટર્મિનલ્સ પર, જો તેમાં વર્તમાન એક એમ્પીયર પ્રતિ સેકન્ડથી બદલાય છે, તો 1 વોલ્ટનો વોલ્ટેજ દેખાશે.

ઇન્ડક્ટન્સની તીવ્રતા બે પરિમાણો પર આધારિત છે: સર્કિટના ભૌમિતિક પરિમાણો (લંબાઈ, પહોળાઈ, વળાંકની સંખ્યા, વગેરે) અને માધ્યમના ચુંબકીય ગુણધર્મો પર (જો, ઉદાહરણ તરીકે, અંદર ફેરાઇટ કોર હોય તો. કોઇલ, તેની ઇન્ડક્ટન્સ વધારે હશે, જો અંદર કોઈ કોર ન હોય તો).

ઉત્પાદિત ઇન્ડક્ટન્સની ગણતરી કરવા માટે, કોઇલ પોતે કેવો આકાર હશે અને તેની અંદરના માધ્યમમાં કઈ ચુંબકીય અભેદ્યતા હશે તે જાણવું જરૂરી છે (માધ્યમની સંબંધિત ચુંબકીય અભેદ્યતા એ શૂન્યાવકાશની ચુંબકીય અભેદ્યતા અને ચુંબકીય અભેદ્યતા વચ્ચેનું પ્રમાણસરતા પરિબળ છે. આપેલ માધ્યમની અભેદ્યતા.અલબત્ત, તે વિવિધ સામગ્રી માટે અલગ છે) ...

ચાલો કોઇલના સૌથી સામાન્ય સ્વરૂપો (નળાકાર સોલેનોઇડ, ટોરોઇડ અને લાંબા વાયર) ના ઇન્ડક્ટન્સની ગણતરી કરવા માટેના સૂત્રો જોઈએ.

ઇન્ડક્ટન્સની ગણતરી કરવા માટેનું સૂત્ર અહીં છે સોલેનોઇડ - કોઇલ, જેની લંબાઈ વ્યાસ કરતા ઘણી વધારે છે:

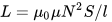
જેમ તમે જોઈ શકો છો, વળાંક N ની સંખ્યા, વિન્ડિંગ l ની લંબાઈ અને કોઇલ S ના ક્રોસ-વિભાગીય વિસ્તારને જાણીને, અમે કોર વિના અથવા કોર સાથે કોઇલની અંદાજિત ઇન્ડક્ટન્સ શોધીએ છીએ, જ્યારે ચુંબકીય શૂન્યાવકાશની અભેદ્યતા એ સતત મૂલ્ય છે:

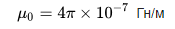
ટોરોઇડલ કોઇલનું ઇન્ડક્ટન્સ, જ્યાં h એ ટોરોઇડની ઊંચાઈ છે, r એ ટોરોઇડનો આંતરિક વ્યાસ છે, R એ ટોરોઇડનો બાહ્ય વ્યાસ છે:

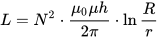
પાતળા વાયરની ઇન્ડક્ટન્સ (ક્રોસ-સેક્શનની ત્રિજ્યા લંબાઈ કરતા ઘણી નાની છે), જ્યાં l એ વાયરની લંબાઈ છે, અને r એ તેના ક્રોસ-સેક્શનની ત્રિજ્યા છે. સૂચકાંકો i અને e સાથે Mu છે આંતરિક (આંતરિક, વાહક સામગ્રી) અને બાહ્ય (બાહ્ય, વાહકની બહારની સામગ્રી) વાતાવરણની સંબંધિત ચુંબકીય અભેદ્યતા:

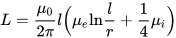
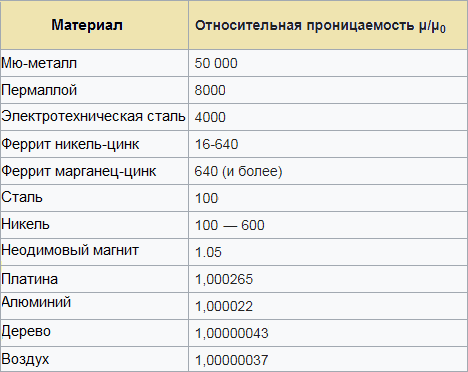
સંબંધિત અનુમતિઓનું કોષ્ટક તમને ચોક્કસ ચુંબકીય સામગ્રીનો ઉપયોગ કરીને સર્કિટ (વાયર, કોઇલ) થી તમે કયા ઇન્ડક્ટન્સની અપેક્ષા રાખી શકો છો તેનો અંદાજ કાઢવામાં મદદ કરશે: