ચુંબકીય ક્ષેત્રની શક્તિ. ચુંબકીય બળ

વાયર અથવા કોઇલની આસપાસ હંમેશા ઇલેક્ટ્રિક પ્રવાહ હોય છે ચુંબકીય ક્ષેત્ર… કાયમી ચુંબકનું ચુંબકીય ક્ષેત્ર અણુમાં તેમની ભ્રમણકક્ષામાં ઇલેક્ટ્રોનની હિલચાલને કારણે થાય છે.

ચુંબકીય ક્ષેત્ર તેની શક્તિ દ્વારા વર્ગીકૃત થયેલ છે. ચુંબકીય ક્ષેત્રની તાકાત H યાંત્રિક શક્તિ જેવી જ છે. તે વેક્ટર જથ્થો છે, એટલે કે, તેની તીવ્રતા અને દિશા છે.

ચુંબકીય ક્ષેત્ર, એટલે કે, ચુંબકની આસપાસની જગ્યા, ચુંબકીય રેખાઓથી ભરેલી તરીકે રજૂ કરી શકાય છે, જે ચુંબકના ઉત્તર ધ્રુવમાંથી બહાર નીકળીને દક્ષિણ ધ્રુવમાં પ્રવેશ કરે છે (ફિગ. 1). ચુંબકીય રેખાના સ્પર્શક ચુંબકીય ક્ષેત્રની તાકાતની દિશા દર્શાવે છે.

ચુંબકીય ક્ષેત્ર વધુ મજબૂત હોય છે જ્યાં ચુંબકીય રેખાઓ વધુ ગીચ હોય છે (ચુંબકના ધ્રુવો પર અથવા વર્તમાન વહન કરતી કોઇલની અંદર).

કોઇલનો વર્તમાન I અને વળાંકની સંખ્યા ω જેટલી વધારે છે, વાયરની નજીક (અથવા કોઇલની અંદર) ચુંબકીય ક્ષેત્ર વધારે છે.

અવકાશમાં કોઈપણ બિંદુએ ચુંબકીય ક્ષેત્ર H ની મજબૂતાઈ ઉત્પાદન ∙ ω જેટલું વધારે છે અને ચુંબકીય રેખાની લંબાઈ જેટલી ટૂંકી છે તેટલી વધારે છે:

H = (I ∙ ω) / l.

તે સમીકરણ પરથી અનુસરે છે કે ચુંબકીય ક્ષેત્રની શક્તિને માપવા માટેનું એકમ એમ્પીયર પ્રતિ મીટર (A/m) છે.

આપેલ સમાન ક્ષેત્રમાં દરેક ચુંબકીય રેખા માટે, ઉત્પાદનો H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω સમાન છે (ફિગ. 1).

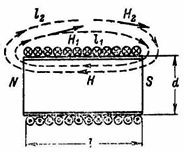
ચોખા. 1.

ચુંબકીય સર્કિટમાં ઉત્પાદન H ∙ l ઇલેક્ટ્રિક સર્કિટમાંના વોલ્ટેજ જેવું જ છે અને તેને ચુંબકીય વોલ્ટેજ કહેવામાં આવે છે, અને ચુંબકીય ઇન્ડક્શન લાઇનની સમગ્ર લંબાઈ સાથે લેવામાં આવે છે તેને ચુંબકીય બળ (ns) Fm કહેવામાં આવે છે: Fm = H ∙ l = હું ∙ ω.

ચુંબકીય બળ Fm એ એમ્પીયરમાં માપવામાં આવે છે, પરંતુ તકનીકી વ્યવહારમાં, એમ્પીયર નામને બદલે, એમ્પીયર-ટર્ન નામનો ઉપયોગ કરવામાં આવે છે, જે ભારપૂર્વક જણાવે છે કે Fm વર્તમાન અને વળાંકની સંખ્યાના પ્રમાણસર છે.

કોર વિનાના નળાકાર કોઇલ માટે, જેની લંબાઈ તેના વ્યાસ (l≫d) કરતા ઘણી વધારે હોય છે, કોઇલની અંદરના ચુંબકીય ક્ષેત્રને સમાન ગણી શકાય, એટલે કે. કોઇલની સમગ્ર આંતરિક જગ્યામાં સમાન ચુંબકીય ક્ષેત્રની તાકાત H સાથે (ફિગ. 1). આવા કોઇલની બહારનું ચુંબકીય ક્ષેત્ર તેની અંદરની તુલનામાં ઘણું નબળું હોવાથી, બાહ્ય ચુંબકીય ક્ષેત્રને અવગણી શકાય છે અને ગણતરીમાં એવું માનવામાં આવે છે કે n. c કોઇલ કોઇલની લંબાઇના ગુણા કોઇલની અંદર ફીલ્ડ સ્ટ્રેન્થના ઉત્પાદનની બરાબર છે.

વાયર અને વર્તમાન કોઇલના ચુંબકીય ક્ષેત્રની ધ્રુવીયતા જીમ્બલ નિયમ દ્વારા નક્કી કરવામાં આવે છે. જો ગિમ્બલની આગળની હિલચાલ વર્તમાનની દિશા સાથે સુસંગત હોય, તો ગિમ્બલ હેન્ડલના પરિભ્રમણની દિશા ચુંબકીય રેખાઓની દિશા સૂચવે છે.

ના ઉદાહરણો

1. 3 A નો પ્રવાહ 2000 વળાંકોની કોઇલમાંથી વહે છે. એન શું છે. વી. કોઇલ?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. કોઇલની ચુંબકીય શક્તિ 6000 એમ્પીયર-ટર્ન છે.

2. 2500 વળાંકની કોઇલમાં n હોવો જોઇએ. p. 10000 A. તેમાંથી કયો પ્રવાહ વહેવો જોઈએ?

I = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.

3.વર્તમાન I = 2 A કોઇલમાંથી વહે છે. n આપવા માટે કોઇલમાં કેટલા વળાંક હોવા જોઈએ. ગામ 8000 A?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 વળાંક.

4. 100 વળાંક સાથે 10 સેમી લાંબી કોઇલની અંદર, ચુંબકીય ક્ષેત્ર H = 4000 A / m ની મજબૂતાઈની ખાતરી કરવી જરૂરી છે. કોઇલમાં કેટલો કરંટ હોવો જોઈએ?

કોઇલનું ચુંબકીય બળ Fm = H ∙ l = I ∙ ω છે. તેથી, 4000 A/m ∙ 0.1 m = I ∙ 100; I = 400/100 = 4 A.

5. કોઇલનો વ્યાસ (સોલેનોઇડ) D = 20 mm છે, અને તેની લંબાઈ l = 10 cm છે. કોઇલ d = 0.4 mm વ્યાસવાળા તાંબાના વાયરમાંથી ઘા છે. જો કોઇલ 4.5V પર ચાલુ કરવામાં આવે તો તેની અંદર ચુંબકીય ક્ષેત્રની શક્તિ કેટલી છે?

ઇન્સ્યુલેશનની જાડાઈને ધ્યાનમાં લીધા વિના વળાંકોની સંખ્યા ω = l∶d = 100∶0.4 = 250 વળાંક.

લૂપ લંબાઈ π ∙ d = 3.14 ∙ 0.02 m = 0.0628 m.

કોઇલ લંબાઈ l1 = 250 ∙ 0.0628 m = 15.7 m.

કોઇલનો સક્રિય પ્રતિકાર r = ρ ∙ l1 / S = 0.0175 ∙ (4 ∙ 15.7) / (3.14 ∙ 0.16) = 2.2 ઓહ્મ.

વર્તમાન I = U/r = 4.5 / 2.2 = 2.045 A ≈2 A.

કોઇલની અંદરના ચુંબકીય ક્ષેત્રની મજબૂતાઈ H = (I ∙ ω) / l = (2 ∙ 250) / 0.1 = 5000 A/m.

6. સીધા વાયરમાંથી 1, 2, 5 સે.મી.ના અંતરે ચુંબકીય ક્ષેત્રની મજબૂતાઈ નક્કી કરો જેના દ્વારા વર્તમાન I = 100 A વહે છે.

ચાલો H ∙ l = I ∙ ω સૂત્રનો ઉપયોગ કરીએ.

સીધા વાયર માટે ω = 1 અને l = 2 ∙ π ∙ r,

જ્યાંથી H = I / (2 ∙ π ∙ r).

H1 = 100 / (2 ∙ 3.14 ∙ 0.01) = 1590 A/m; H2 = 795 A/m; H3 = 318 A/m.