ચુંબકીય સર્કિટની ગણતરીઓ

વિદ્યુત મશીનો અને ઉપકરણમાં, ચુંબકીય પ્રવાહ F ચુંબકીય સર્કિટ (ફેરોમેગ્નેટિક કોર) અને આ ચુંબકીય સર્કિટના હવાના અંતરમાં કેન્દ્રિત છે. ચુંબકીય પ્રવાહના આ માર્ગને ચુંબકીય સર્કિટ કહેવામાં આવે છે.

ચુંબકીય સર્કિટ ઇલેક્ટ્રિકલ સર્કિટ જેવું છે. ચુંબકીય પ્રવાહ Ф ઇલેક્ટ્રિક પ્રવાહ I જેવું લાગે છે, ઇન્ડક્શન В વર્તમાન ઘનતા જેવું લાગે છે, ચુંબકીય બળ (ns) Fн (H ∙ l = I ∙ ω) e ને અનુરૂપ છે. વગેરે સાથે

સૌથી સરળ કિસ્સામાં, ચુંબકીય સર્કિટમાં દરેક જગ્યાએ સમાન ક્રોસ-સેક્શન હોય છે અને તે સજાતીય ચુંબકીય સામગ્રીથી બનેલું હોય છે. n નક્કી કરવા માટે. l ∙ ω સાથે જરૂરી ઇન્ડક્શન B પ્રદાન કરવા માટે જરૂરી છે, અનુરૂપ તીવ્રતા H ચુંબકીયકરણ વળાંક પરથી નક્કી કરવામાં આવે છે અને ચુંબકીય ક્ષેત્ર રેખા l ની સરેરાશ લંબાઈ દ્વારા ગુણાકાર કરવામાં આવે છે: H ∙ l = I ∙ ω = Fm.

અહીંથી, આવશ્યક પ્રવાહ I અથવા કોઇલના વળાંકોની સંખ્યા ω નક્કી થાય છે.

જટિલ ચુંબકીય સર્કિટમાં સામાન્ય રીતે વિવિધ વિભાગો અને ચુંબકીય સામગ્રીવાળા વિભાગો હોય છે. આ વિભાગો સામાન્ય રીતે શ્રેણીમાં જોડાયેલા હોય છે, તેથી સમાન ચુંબકીય પ્રવાહ F તેમાંથી દરેકમાંથી પસાર થાય છે.દરેક વિભાગમાં ઇન્ડક્શન B વિભાગના ક્રોસ-સેક્શન પર આધાર રાખે છે અને સૂત્ર B = Φ∶S દ્વારા દરેક વિભાગ માટે અલગથી ગણવામાં આવે છે.

ઇન્ડક્શનના વિવિધ મૂલ્યો માટે, તીવ્રતા H ચુંબકીયકરણ વળાંકથી નક્કી કરવામાં આવે છે અને સર્કિટના અનુરૂપ વિભાગની પાવર લાઇનની સરેરાશ લંબાઈથી ગુણાકાર કરવામાં આવે છે. વ્યક્તિગત કાર્યોનો સારાંશ આપતાં, વ્યક્તિને સંપૂર્ણ n મળે છે. c. ચુંબકીય સર્કિટ:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … જે ચુંબકીય પ્રવાહ અથવા કોઇલ વળાંકની સંખ્યા નક્કી કરે છે.

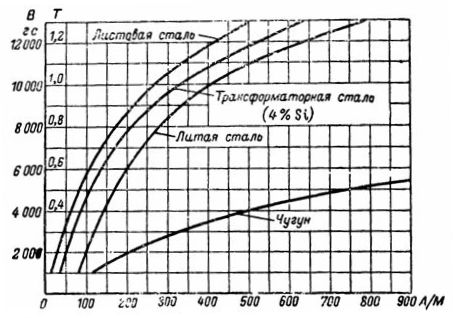
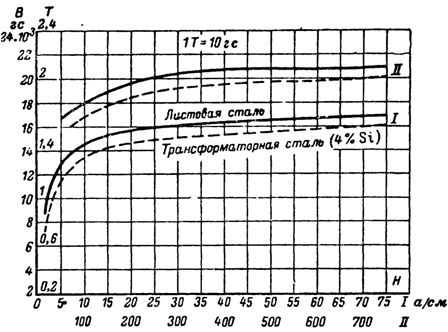
ચુંબકીકરણ વણાંકો

ના ઉદાહરણો

1. 200 વળાંકની કોઇલનો ચુંબકીય પ્રવાહ I શું હોવો જોઈએ જેથી n. c. કાસ્ટ આયર્ન રીંગમાં બનાવેલ ચુંબકીય પ્રવાહ Ф = 15700 Ms = 0.000157 Wb? કાસ્ટ આયર્ન રિંગની સરેરાશ ત્રિજ્યા r = 5 સેમી છે, અને તેના વિભાગનો વ્યાસ d = 2 સેમી (ફિગ. 1) છે.

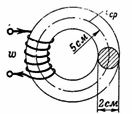
ચોખા. 1.

ચુંબકીય સર્કિટનો વિભાગ S = (π ∙ d ^ 2) / 4 = 3.14 cm2.

કોરમાં ઇન્ડક્શન છે: B = Φ∶S = 15700∶3.14 = 5000 G.

MKSA સિસ્ટમમાં, ઇન્ડક્શન છે: B = 0.000157 Wb: 0.0000314 m2 = 0.5 T.

કાસ્ટ આયર્નના ચુંબકીયકરણ વળાંકમાંથી, અમને B = 5000 G = 0.5 T માટે 750 A/m ની બરાબર જરૂરી તાકાત H મળે છે. ચુંબકીકરણ શક્તિ બરાબર છે: I ∙ ω = H ∙ l = 235.5 Av.

તેથી, જરૂરી વર્તમાન I = (H ∙ l) / ω = 235.5 / 200 = 1.17 A.

2. બંધ ચુંબકીય સર્કિટ (ફિગ. 2) ટ્રાન્સફોર્મરની સ્ટીલ પ્લેટોથી બનેલી છે. કોર Ф = 160000 Ms = 0.0016 Wb માં ચુંબકીય પ્રવાહ બનાવવા માટે 0.5 A ના પ્રવાહ સાથે કોઇલમાં કેટલા વળાંક હોવા જોઈએ?

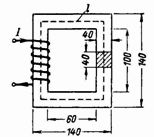
ચોખા. 2.

કોર વિભાગ S = 4 ∙ 4 = 16 cm2 = 0.0016 m2.

કોર ઇન્ડક્શન B = F/S = 160000/16 = 10000 Gs = 1 T.

ટ્રાન્સફોર્મર સ્ટીલના ચુંબકીયકરણ વળાંક મુજબ, આપણે B = 10,000 Gs = 1 T માટે શોધીએ છીએ તીવ્રતા H = 3.25 A/cm = 325 A/m.

ચુંબકીય ક્ષેત્ર રેખાની સરેરાશ લંબાઈ l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 મીટર છે.

ચુંબકીય બળ Fm = I ∙ ω = H ∙ l = 3.25 ∙ 48 = 315 ∙ 0.48 = 156 Av.

0.5 A ના પ્રવાહ પર, વળાંકની સંખ્યા ω = 156 / 0.5 = 312 છે.

3. ફિગમાં બતાવેલ ચુંબકીય સર્કિટ. 3 એ અગાઉના ઉદાહરણના ચુંબકીય સર્કિટ જેવું જ છે, સિવાય કે તેમાં δ = 5 mm નું હવાનું અંતર છે. શું હોવું જોઈએ. s. અને કોઇલ પ્રવાહ કે જેથી ચુંબકીય પ્રવાહ અગાઉના ઉદાહરણની જેમ જ હોય, એટલે કે F = 160000 Ms = 0.0016 Wb?

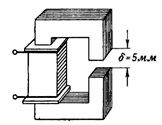
ચોખા. 3.

ચુંબકીય સર્કિટમાં બે શ્રેણી-જોડાયેલા વિભાગો છે, જેનો ક્રોસ-સેક્શન અગાઉના ઉદાહરણની જેમ જ છે, એટલે કે S = 16 cm2. ઇન્ડક્ટન્સ પણ B = 10000 G = 1 T બરાબર છે.

સ્ટીલની ચુંબકીય રેખાની સરેરાશ લંબાઈ થોડી ઓછી છે: lс = 48-0.5 = 47.5 cm ≈0.48 m.

ચુંબકીય સર્કિટના આ વિભાગમાં ચુંબકીય વોલ્ટેજ Hc ∙ lc = 3.25 ∙ 48≈156 Av છે.

હવાના અંતરમાં ક્ષેત્રની તાકાત છે: Hδ = 0.8 ∙ B = 0.8 ∙ 10000 = 8000 A/cm.

એર ગેપના ક્રોસ-સેક્શનમાં ચુંબકીય તણાવ Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av.

પૂર્ણ એન. c. વ્યક્તિગત વિભાગોમાં ચુંબકીય વોલ્ટેજના સરવાળા સમાન છે: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13.3 A.

જો અગાઉના ઉદાહરણમાં જરૂરી ચુંબકીય પ્રવાહ 0.5 A ના પ્રવાહ દ્વારા પ્રદાન કરવામાં આવ્યો હતો, તો પછી 0.5 સે.મી.ના હવાના અંતર સાથેના ચુંબકીય સર્કિટ માટે સમાન ચુંબકીય પ્રવાહ મેળવવા માટે 13 A નો પ્રવાહ જરૂરી છે. આના પરથી જોઈ શકાય છે કે હવાનું અંતર, ચુંબકીય સર્કિટની લંબાઈના સંબંધમાં પણ નજીવું, જરૂરી n ને ખૂબ વધારે છે. v. અને કોઇલ પ્રવાહ.

4. ટ્રાન્સફોર્મરનો ચુંબકીય પ્રવાહ F = 72000 Ms તરીકે ગણવામાં આવે છે. n ની ગણતરી જરૂરી છે.s.અને 800 વળાંક ધરાવતા પ્રાથમિક વિન્ડિંગનો ચુંબકીય પ્રવાહ. ટ્રાન્સફોર્મરના કોરમાં ગેપ δ = 0.2 mm છે. ટ્રાન્સફોર્મર કોરના પરિમાણો ફિગમાં બતાવવામાં આવ્યા છે. 4. કોર S = 2 ∙ 3 ​​​ = 6 cm2 (આ આકારના કોરોવાળા ટ્રાન્સફોર્મર્સને આર્મર્ડ કહેવામાં આવે છે) નો ક્રોસ સેક્શન.

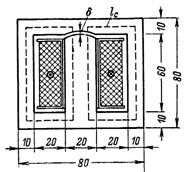
ચોખા. 4.

કોર અને એર ગેપ ઇન્ડક્શન B = F/S = 72000/6 = 12000 G.

B = 12000 G માટે ટ્રાન્સફોર્મર સ્ટીલના ચુંબકીયકરણ વળાંક અનુસાર, અમે તીવ્રતા નક્કી કરીએ છીએ: Hc = 5 A / cm.

સ્ટીલમાં ચુંબકીય રેખાની સરેરાશ લંબાઈ lс = 2 ∙ (6 + 3) = 18 cm છે.

હવાના અંતરમાં વોલ્ટેજ Hδ = 0.8 ∙ B = 9600 A/cm.

ચુંબકીય બળ I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0.02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0.35 A.

આર્મર્ડ કોરમાં, ચુંબકીય પ્રવાહ બે ભાગોમાં વિભાજિત થાય છે, જે બાજુના સળિયા સાથે બંધ હોય છે, જેનો ક્રોસ વિભાગ S/2 છે, અને ચુંબકીય રેખાની સરેરાશ લંબાઈ એલસી છે. પરિણામે, ચુંબકીય સર્કિટ સામાન્ય કોર S અને પાવર લાઇન એલસીની લંબાઈવાળા પરંપરાગત ટ્રાન્સફોર્મરના ચુંબકીય સર્કિટ સાથે સંપૂર્ણપણે સમાન છે.

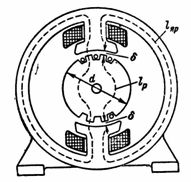
5. DC મશીન F = 1280000 Mks નો ચુંબકીય પ્રવાહ. ચુંબકીય સર્કિટમાં સરેરાશ ચુંબકીય રેખા લંબાઈ lа = 80 cm સાથે કાસ્ટ સ્ટીલ યોક, સરેરાશ ક્ષેત્ર લંબાઈ lр = 18 cm સાથે ઇલેક્ટ્રિક સ્ટીલ પ્લેટ્સમાંથી એસેમ્બલ કરાયેલ રોટર અને બે એર ગેપ્સ δ 0.2 cm દરેક ધરાવે છે. = 8 ∙ 20 સેમી 2; રોટર અને ધ્રુવ વિભાગ Sр = 12 ∙ 20 cm2... n ગણતરી કરો. p. અને ધ્રુવ કોઇલના વળાંકોની સંખ્યા, જો તેમાં મહત્તમ ચુંબકીય (ઉત્સાહક) પ્રવાહ 1 A (ફિગ. 5) હોય.

ચોખા. 5.

યોક અને ધ્રુવમાં ઇન્ડક્શન Bя = Ф / Sя = 1280000/160 = 8000 G.

Bя = 8000 G પર કાસ્ટ સ્ટીલના ચુંબકીયકરણ વળાંક અનુસાર યોક અને ધ્રુવમાં વોલ્ટેજ બરાબર છે:

H = 2.8 A / cm.

યોકના વિભાગમાં ચુંબકીકરણનું બળ HЯ ∙ la = 2.8 ∙ 80 = 224 Av.

રોટર, પોલ અને એર ગેપમાં ઇન્ડક્શન Br = Ф / Ср = 1280000/240 = 5333 G.

સ્ટીલ પ્લેટથી બનેલા રોટરમાં વોલ્ટેજ Br = 5333 Gs Hrp = 0.9 A/cm,

અને રોટર વિભાગનું ચુંબકીય વોલ્ટેજ Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av.

હવાના અંતરમાં વોલ્ટેજ Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A/cm.

એર ગેપના ક્રોસ સેક્શનમાં ચુંબકીય વોલ્ટેજ Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 A.

પૂર્ણ એન. c. અલગ-અલગ વિભાગોમાં ચુંબકીય વોલ્ટેજના સરવાળાની બરાબર: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 Av.

બે ધ્રુવ કોઇલમાં વળાંકની સંખ્યા ω = (I ∙ ω) / I = 1946.76 / 1≈2000.