ઇન્ડક્શન મોટરની કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ

ઇન્ડક્શન મોટરની કૃત્રિમ લાક્ષણિકતાઓ સપ્લાય વોલ્ટેજ, સપ્લાય ફ્રીક્વન્સીમાં ફેરફાર કરીને, સ્ટેટર અને રોટર સર્કિટમાં વધારાના પ્રતિકાર રજૂ કરીને મેળવવામાં આવે છે.

સપ્લાય વોલ્ટેજને બદલીને મેળવેલ કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ. કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ સાથે કાર્યકારી શાખા બનાવવા માટે, બે મુદ્દાઓ ધ્યાનમાં લો. પ્રથમ 1 બિંદુ સિંક્રનસ કોણીય વેગને અનુરૂપ છે, બીજો 2 - મહત્તમ (જટિલ) ક્ષણ (ફિગ. 1) સાથે.

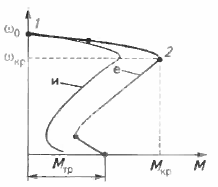
ચોખા. 1. જ્યારે મેઈન વોલ્ટેજ બદલાય છે ત્યારે અસુમેળ મોટરની યાંત્રિક લાક્ષણિકતાઓ: e — નજીવા મેઈન વોલ્ટેજ (Unom) પર કુદરતી લાક્ષણિકતા અને ઘટાડેલા મેઈન વોલ્ટેજ પર કૃત્રિમ લાક્ષણિકતા છે (Ufact = 0.9Unom); ωo — સિંક્રનસ કોણીય વેગ; Mtr, Mkr — અનુક્રમે એન્જિનની શરૂઆત અને નિર્ણાયક ક્ષણ.

ઇન્ડક્શન મોટરનો સિંક્રનસ કોણીય વેગ છે:

ωo = 2πf / p

આ સૂત્રમાંથી જોઈ શકાય છે તેમ, સિંક્રનસ કોણીય વેગ વોલ્ટેજ પર આધારિત નથી. તેથી, y-અક્ષ સાથે તેની સ્થિતિ બદલાતી નથી.બીજા બિંદુમાં કોઓર્ડિનેટ્સ છે: નિર્ણાયક ક્ષણ અને નિર્ણાયક કોણીય વેગ. નિર્ણાયક કોણીય વેગ વોલ્ટેજથી સ્વતંત્ર છે, અને નિર્ણાયક ક્ષણ વાસ્તવિક વોલ્ટેજના વર્ગના પ્રમાણસર છે, એટલે કે. U2 હકીકત.

ઉદાહરણ તરીકે, જો મુખ્ય વોલ્ટેજમાં 10% ઘટાડો થાય છે, તો વાસ્તવિક વોલ્ટેજ 90% અથવા Uactual = 0.9Unom હશે. તેથી, કૃત્રિમ લાક્ષણિકતા પર નિર્ણાયક ક્ષણ પ્રમાણસર છે

Mkr.isk ~U2fact ~ (0.9Unom)2 ~ 0.81U2fact

Mkr.isk શોધવા માટે, અમે પ્રમાણ બનાવીશું:

Mkr.est. ~U2nom;

Mkr.isk ~ 0.81U2 હકીકત.

તેથી:

Mkr.isk = Mkr.est. x (0.81U2actual/U2nom) = 0.81Mcr.

ગ્રાફ પર (જુઓ. ફિગ. 1) અમે Mkr.est ના 81% ને અનુરૂપ બિંદુને મુલતવી રાખીએ છીએ. અને કૃત્રિમ યાંત્રિક લાક્ષણિકતાનું નિર્માણ.

કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ ઇન્ડક્શન મોટરના રોટર સર્કિટમાં ઘા રોટર (આર સુધી 6) સાથે વધારાના પ્રતિકારની રજૂઆત દ્વારા મેળવવામાં આવે છે.

કૃત્રિમ યાંત્રિક લાક્ષણિકતા બનાવવા માટે, બે બિંદુઓ (ફિગ. 2) ધ્યાનમાં લો.

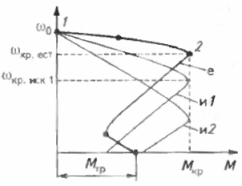
ચોખા. 2. રોટર સર્કિટમાં વધારાના પ્રતિકારનો પરિચય કરતી વખતે અસુમેળ મોટરની યાંત્રિક લાક્ષણિકતાઓ: e — Radd = 0 પર ગણતરી કરેલ કુદરતી લાક્ષણિકતા; અને 1 — કૃત્રિમ લક્ષણ જ્યારે Rext1 0 ની બરાબર નથી; u2 — Radd2 > Rad1 માં કૃત્રિમ લાક્ષણિકતા; ωcr.fed — કુદરતી લાક્ષણિકતાનો નિર્ણાયક કોણીય વેગ; ωcr.isk — કૃત્રિમ લાક્ષણિકતાનો નિર્ણાયક કોણીય વેગ; M;tr, અનુક્રમે MCR નો સ્ટાર્ટિંગ ટોર્ક અને મોટરનો ક્રિટિકલ ટોર્ક.

સિંક્રનસ કોણીય વેગ (પ્રથમ બિંદુ 1) સૂત્ર ωо = 2πf/p... દ્વારા નક્કી થાય છે... તે વધારાના પ્રતિકાર પર આધાર રાખે છે. તેથી પ્રથમ મુદ્દો રહે છે.બીજા બિંદુ 2 માં કોઓર્ડિનેટ્સ છે: ક્ષણ મહત્વપૂર્ણ છે અને વેગ મહત્વપૂર્ણ છે.

નિર્ણાયક ગતિ વધારાના પ્રતિકારના વિપરીત પ્રમાણસર છે અને નિર્ણાયક ક્ષણ વધારાના પ્રતિકારથી સ્વતંત્ર છે

આ મોડની યાંત્રિક લાક્ષણિકતાઓ આકૃતિ 2 માં દર્શાવવામાં આવી છે. સપ્લાય વોલ્ટેજની આવર્તન બદલીને મેળવેલ કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ. કૃત્રિમ યાંત્રિક લાક્ષણિકતા બનાવવા માટે, બે મુદ્દાઓ (ફિગ. 3) ધ્યાનમાં લો.

સિંક્રનસ કોણીય વેગ (પ્રથમ બિંદુ) સૂત્ર ωо = 2πf/p દ્વારા નક્કી કરવામાં આવે છે. તે સપ્લાય વોલ્ટેજની આવર્તન સાથે સીધી પ્રમાણમાં છે. તેથી, પ્રથમ બિંદુ ઓર્ડિનેટ અક્ષ સાથે ખસેડવામાં આવશે.

બીજા બિંદુમાં કોઓર્ડિનેટ્સ છે: ક્ષણ નિર્ણાયક છે અને વેગ મહત્વપૂર્ણ છે. નિર્ણાયક ગતિ સપ્લાય વોલ્ટેજની આવર્તન સાથે સીધી પ્રમાણસર છે અને નિર્ણાયક ક્ષણ સપ્લાય વોલ્ટેજની આવર્તનના વર્ગ સાથે સીધી પ્રમાણમાં છે.

આકૃતિ 3 ઘટતા સપ્લાય વોલ્ટેજ આવર્તન સાથે ઇન્ડક્શન મોટરની કુદરતી અને કૃત્રિમ યાંત્રિક લાક્ષણિકતાઓ દર્શાવે છે.

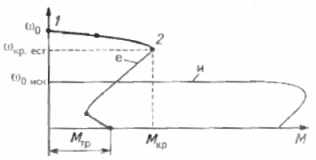
ચોખા. 3. પાવર સપ્લાય ફ્રીક્વન્સીમાં ઘટાડા સાથે અસુમેળ મોટરની યાંત્રિક લાક્ષણિકતાઓ: e — 50 Hz પર કુદરતી લાક્ષણિકતા અને 0.5 ehranse પર eisk પર કૃત્રિમ લાક્ષણિકતા છે; ωo — કુદરતી લાક્ષણિકતાનો સિંક્રનસ કોણીય વેગ; ω શોધ — કૃત્રિમ લાક્ષણિકતાની સિંક્રનસ કોણીય વેગ; ωક્રોસ — કુદરતી લાક્ષણિકતાનો નિર્ણાયક કોણીય વેગ; Mtr, Mkr — અનુક્રમે એન્જિનની શરૂઆતની ક્ષણ અને નિર્ણાયક ક્ષણ.